Выпуклая оболочка системы точек
Определение.Точка 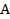 называется выпуклой комбинацией точек А1, А2, …,Аm, если существуют такие числа
называется выпуклой комбинацией точек А1, А2, …,Аm, если существуют такие числа  , что
, что 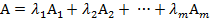 при условии
при условии 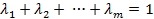 .
.
Например, любая внутренняя точка круга является выпуклой комбинацией концов хорды, проходящей через эту точку.
Представим себе, что в плоскость, имеющую вид бесконечного листа фанеры, в некоторых точках А1, А2, …, Аm забиты колышки. Если резиновой петлёй охватить все колышки, то получим многоугольную область с вершинами в некоторых из точек А1, А2, …,Аm, которая на рисунке отмечена штриховкой. Эта область называется выпуклой оболочкой системы точек А1, А2, …,Аm.
А2
| А6 |
А6
А5 А4
Более строгое определение выпуклой оболочки.
Определение.Множество всех выпуклых линейных комбинаций точек А1, А2, …,Аm называется выпуклой оболочкойсистемы точек А1, А2, …,Аm и обозначается
<А1, А2, …,Аm >
Пример 5.4.1. Выразить точку 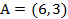 в виде выпуклой комбинации угловых точек множества
в виде выпуклой комбинации угловых точек множества  пространства
пространства 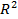 , заданного системой неравенств
, заданного системой неравенств
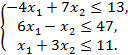
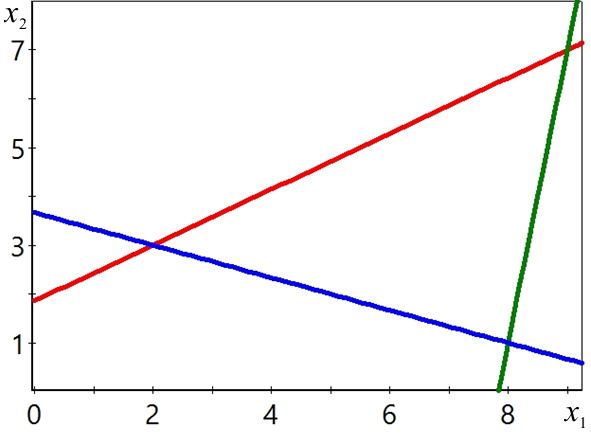
Решение. Множество  выпукло и представляет собой треугольник с вершинами
выпукло и представляет собой треугольник с вершинами 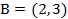 ,
, 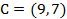 ,
, 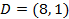 . Здесь, координаты вершин являются точками пересечения прямых:
. Здесь, координаты вершин являются точками пересечения прямых:
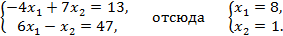
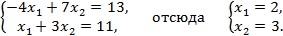
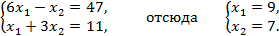
Представим точку 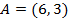 в виде следующей выпуклой комбинации:
в виде следующей выпуклой комбинации:
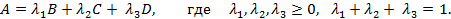
В координатной форме получим два уравнения:
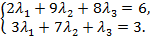
Добавим к ним условие 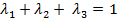 , получим систему трех линейных уравнений с тремя неизвестными. Решим систему трех уравнений методом Гаусса:
, получим систему трех линейных уравнений с тремя неизвестными. Решим систему трех уравнений методом Гаусса:
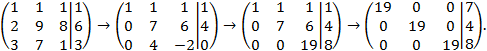
Отсюда получаем значения
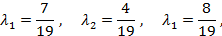
удовлетворяющие условию неотрицательности: 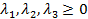 . Поэтому искомое представление имеет вид:
. Поэтому искомое представление имеет вид:
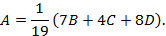
Ответ: Точка 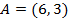 может быть представлена выпуклой комбинацией угловых точек множества
может быть представлена выпуклой комбинацией угловых точек множества  пространства
пространства 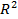 , заданного системой неравенств
, заданного системой неравенств
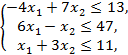
в виде:
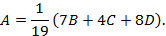
Дата добавления: 2016-10-17; просмотров: 1486;
