Собственные значения и собственные векторы линейных операторов
Определение.Ненулевой вектор 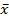 линейного пространства V называется собственным вектором линейного преобразования f , если выполняется равенство
линейного пространства V называется собственным вектором линейного преобразования f , если выполняется равенство
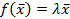 , (5.4)
, (5.4)
где 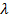 – некоторое число. При этом число
– некоторое число. При этом число 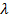 называется собственным значениемлинейного преобразования f. Говорят также, что
называется собственным значениемлинейного преобразования f. Говорят также, что 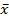 есть собственный вектор,принадлежащийсобственному значению
есть собственный вектор,принадлежащийсобственному значению 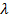 .
.
Пусть А – матрица линейного преобразования f в базисе 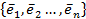 и Х - матрица-столбец из координат вектора
и Х - матрица-столбец из координат вектора 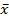 , тогда соотношение (5.4) может быть записано в матричной форме
, тогда соотношение (5.4) может быть записано в матричной форме
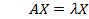 . (5.5)
. (5.5)
Принято говорить, что ненулевая матрица-столбец Х является собственным вектором квадратной матрицы А, соответствующим собственному значению 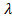 .
.
Уравнение (5.5) может быть переписано в виде
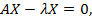
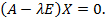
Однородная система уравнений тогда и только тогда имеет ненулевое решение, когда её определитель равен нулю, т.е.
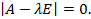 (5.6)
(5.6)
Определение.Уравнение (5.6) называется характеристическим уравнением матрицы А.
Таким образом, собственные значения матрицы А являются корнями её характеристического уравнения.
Предложение.Собственные значения матриц А и АТ совпадают.
Пример. Найти собственные значения и собственные векторы матрицы
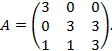
Решение. Запишем характеристическое уравнение
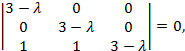
или 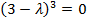 . Следовательно,
. Следовательно, 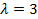 – единственное собственное значение матрицы А. Система уравнений для отыскания собственных векторов сводится к единственному уравнению
– единственное собственное значение матрицы А. Система уравнений для отыскания собственных векторов сводится к единственному уравнению
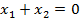 ,
,
или 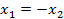 . Положим
. Положим 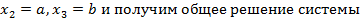
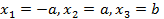 , то ест собственный вектор
, то ест собственный вектор 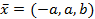 представляется в виде линейной комбинации
представляется в виде линейной комбинации
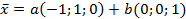
двух линейно независимых векторов 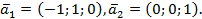
Замечание.Одному собственному значению может соответствовать несколько линейно независимых собственных векторов.
Пример. Найти собственные векторы и собственные значения матрицы
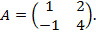
Решение. Запишем характеристическое уравнение
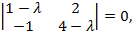
или 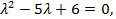 откуда
откуда 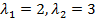 . Найдём собственные векторы. Подставим
. Найдём собственные векторы. Подставим 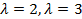 в систему уравнений
в систему уравнений 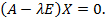
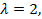
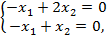
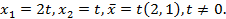
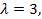
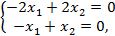
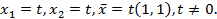
Зависимость между матрицами одного и того же оператора в разных базисах выражается теоремой.
Теорема.Матрицы А и А* линейного оператора 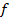 в базисах
в базисах 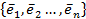 и
и 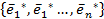 связаны соотношением
связаны соотношением
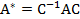
где С – матрица перехода от старого базиса к новому.
Пример. В базисе 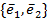 оператор f имеет матрицу
оператор f имеет матрицу 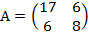 . Найти матрицу оператора в новом базисе
. Найти матрицу оператора в новом базисе 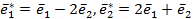 .
.
Решение. Матрица перехода здесь 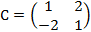 , а обратная к ней матрица
, а обратная к ней матрица 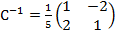 . Следовательно по формуле выше имеем
. Следовательно по формуле выше имеем
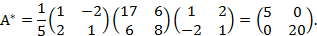
Квадратичные формы
Определение.Квадратичной формой 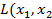 ,…,
,…, 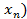 от п переменных называется сумма, каждый член которой является либо квадратом одной из этих переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
от п переменных называется сумма, каждый член которой является либо квадратом одной из этих переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
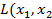 ,…,
,…, 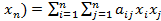 . (5.7)
. (5.7)
Коэффициенты 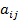 – действительные числа, причём
– действительные числа, причём 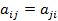 . Матрица А = (
. Матрица А = ( 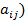 , составленная из этих коэффициентов, называется матрицей квадратичной формы.
, составленная из этих коэффициентов, называется матрицей квадратичной формы.
В матричной записи квадратичная форма имеет вид
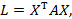
где Х – вектор-столбец переменных.
То есть
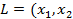 ,…,
,…, 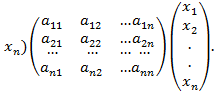
Пример. Дана квадратичная форма 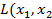 ,
, 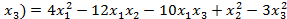 . Записать её в матричном виде.
. Записать её в матричном виде.
Решение. На диагонали лежат коэффициенты при квадратах переменных, а другие элементы – половинам соответствующих коэффициентам квадратичной формы. Следовательно,
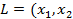 ,
, 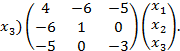
Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных.
Пусть вектор-столбцы переменных X и Y связаны линейным соотношением 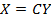 , где
, где 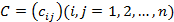 есть некоторая невырожденная матрица п-го порядка. Тогда квадратичная форма
есть некоторая невырожденная матрица п-го порядка. Тогда квадратичная форма
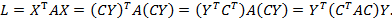
Итак, при невырожденном линейном преобразовании 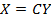 матрица квадратичной формы имеет вид
матрица квадратичной формы имеет вид
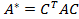 (5.8)
(5.8)
Формулы 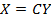 можно истолковывать как формулы преобразования координат вектора при переходе к новому базису, поэтому равенство (5.8) можно рассматривать ка выражение для матрицы квадратичной формы L в новом базисе.
можно истолковывать как формулы преобразования координат вектора при переходе к новому базису, поэтому равенство (5.8) можно рассматривать ка выражение для матрицы квадратичной формы L в новом базисе.
Пример.Дана квадратичная форма 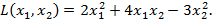 Найти квадратичную форму
Найти квадратичную форму 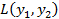 , полученную из данной, линейным преобразованием
, полученную из данной, линейным преобразованием 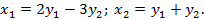
Решение. Матрица квадратичной формы 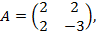 а матрица линейного преобразования
а матрица линейного преобразования 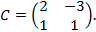
Следовательно, по формуле (5.8) матрица искомой квадратичной формы
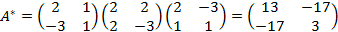 ,
,
а квадратичная форма имеет вид 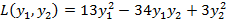 .
.
Определение.Каноническим видом квадратичной формы называется выражение
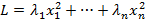 .
.
Особенность этого вида в том, что отсутствуют члены с произведением различных координат.
Определение. Нормальным видом квадратичной формы называется выражение
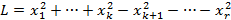 .
.
Этот вид характеризуется тем, что входящие в него квадраты переменных имеют коэффициенты плюс или минус единица. Количество слагаемых в этой формуле равно рангу  квадратичной формы.
квадратичной формы.
Метод Лагранжа
Метод Лагранжа – это метод последовательного выделения полных квадратов квадратичной формы. Например, если 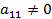 , выделим слагаемые, содержащие
, выделим слагаемые, содержащие 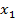 . Слагаемые, не содержащие
. Слагаемые, не содержащие 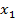 , обозначим как
, обозначим как 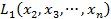 .
.
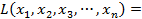
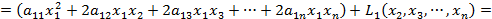
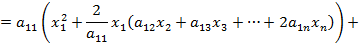
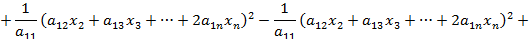
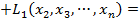
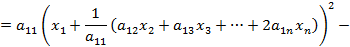
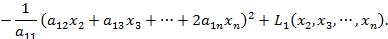
Итак, первое слагаемое представляет собой полный квадрат некоторого выражения, содержащего 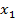 . Затем подобную процедуру проделаем с квадратичной формой
. Затем подобную процедуру проделаем с квадратичной формой
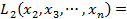
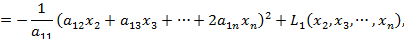
выделив в ней полный квадрат некоторого выражения, содержащего 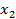 , и т.д. Если
, и т.д. Если 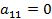 , то после предварительной замены переменных
, то после предварительной замены переменных
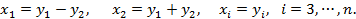
преобразование сводится к рассмотренной процедуре.
Дата добавления: 2016-10-17; просмотров: 4547;
