Нахождение ранга матрицы
Ранг матрицы 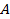 находят либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор
находят либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор 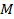 k-го порядка матрицы
k-го порядка матрицы 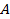 , отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор
, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор 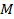 , т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен
, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен 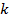 .
.
3. Критерий существования ненулевых решений однородной системы линейных алгебраических уравнений с n неизвестными, состоящей из n уравнений
Для того, чтобы однородная система 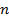 линейных уравнений с
линейных уравнений с 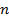 неизвестными (матрица системы A – квадратная) имела нетривиальное решение, необходимо и достаточно, чтобы определитель матрицы этой системы был равен нулю:
неизвестными (матрица системы A – квадратная) имела нетривиальное решение, необходимо и достаточно, чтобы определитель матрицы этой системы был равен нулю: 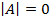 .
.
Нахождение обратной матрицы
Теорема. Если 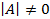 , то матрица
, то матрица
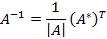
является обратной для А, где матрица  называется присоединённой для А.
называется присоединённой для А.
Пример.Проверить, что матрица
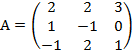
является невырожденной, и найти 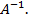
Решение. 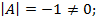
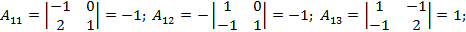


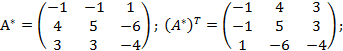
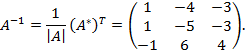
Дата добавления: 2016-10-17; просмотров: 719;
