Геометрическое изображение комплексных чисел
Изображениями комплексных чисел служат точки координатной плоскости. Каждому комплексному числу z = a + bi в декартовой системе координат будет отвечать точка с координатами (a, b). Эту точку чаще всего обозначают той же буквой z, что и само число; вместо слов «число z» говорят «точка z». Ось Ох называют действительной осью. Ось Оу – мнимой осью.
Плоскость, точки которой интерпретируются как изображения комплексных чисел, называется комплексной плоскостью.
2. Модуль и аргумент комплексного числа
Каждому комплексному числу ставится в соответствие вектор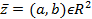 
.
Y
b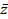 
φ
0 a Х
Преимущество такой интерпретации заключается в том, что операции над векторами в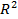 
согласованы с операциями сложения комплексных чисел и умножения на действительное число. Действительно, пусть комплексным числам z1 = a1 + b1i и z2 = a2 + b2i соответствуют векторы 
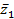=(a1 , b1)и 
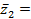(a2 , b2). Тогда сумме z1 + z2 будет соответствовать вектор 
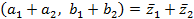, а произведению 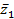на действительное число a – вектор 
.
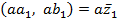Определение. Длину вектора 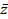, соответствующего комплексному числу 
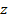, называют модулем этого числа 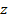. Угол φ между вектором 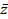и положительным направлением оси Ох называют аргументом комплексного числа .
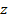Обозначают модуль -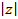 
, аргумент - 
.
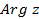Если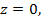 
то 
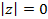, а 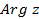не определен.
Аргумент комплексного числа определен с точностью до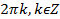 
. Значение аргумента, заключённое в промежутке 
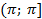, обозначается arg 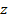и называется главным значениме аргумента.
Пусть z = a + bi - отличное от нуля комплексное число. Из определения следует, что
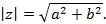
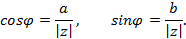
Из формул следует тригонометрическая запись комплексного числа
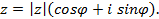
Если z – действительное число, т.е. z = a + 0∙i , то
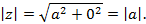
Таким образом, понятие модуля комплексного числа является обобщением понятия действительного числа.
Пример.Представить в тригонометрической форме число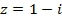 
.
Решение. Вычислим модуль z: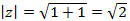 
. Тогда
).
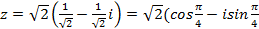Тригонометрическую форму удобно использовать для выполнения операций умножения и деления комплексных чисел.
Пусть
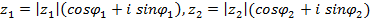
- комплексные числа, заданные в тригонометрической форме. Тогда получим
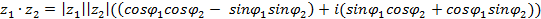
Следовательно,
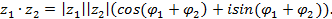
Используя метод математической индукции, можно распространить формулу на любое число сомножителе:
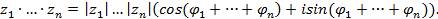(4.1)
Деление
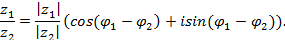
Чтобы вычислить п – ю степень комплексного числа 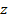, положим в формуле (4.1)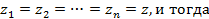 
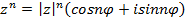
или
.
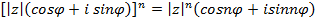Эта формула называется формулой Муавра.
Пример.Вычислить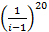 
.
Решение. Найдём тригонометрическую форму числа.
.
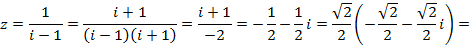
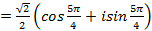Тогда по формуле Муавра находим
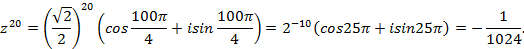
3.2.Корни n-ой степени из комплексного числа. Формулировка основной теоремы алгебры.
Корнем п-й степени из комплексного числа 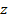называется комплексное число и такое, что
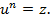(4.2)
Пусть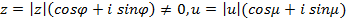 
.
Используя формулу Муавра и (4.2), находим
.
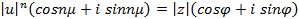Отсюда следует, что
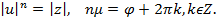
Из первого равенства находим
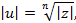
из второго
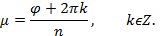
Таким образом, корни п -й степени вычисляются по формуле
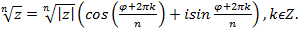(4.3)
Так как аргумент определен с точностью до 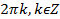, то для корня имеется ровно п различных значений, и чтобы получить эти значения, достаточно в правой части формулы положить k равным 0, 1, 2,…, п – 1.
Из (4.3) следует, что точки, соответствующие значениям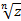 
, расположены на окружности радиуса 
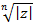с центром в начале координат и делят окружность на п равных частей.
Пример.Решить уравнение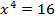 
.
Решение. У данного уравнения на множестве комплексных чисел существует 4 корня. Чтобы их найти, представим его в тригонометрической форме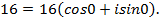 
Тогда
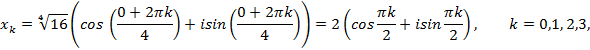
Т.е.
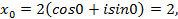
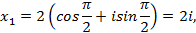
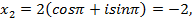
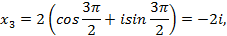
Многочлены
Определение.Функция
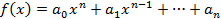
(где п – целое число), называется многочленом(полиномом) или целой рациональной функцией от х. Число п называется степенью многочлена. Здесь коэффициенты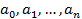 
( 
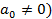– действительные или комплексные числа, а переменная х также может принимать как действительные, так и комплексные значения.
Корнем многочлена называется такое значение х, при котором многочлен обращается в нуль.
Теорема Безу. Остаток от деления многочлена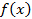 
на двучлен х – 
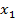равен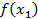 
.
Следствие.Если 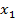– корень многочлена 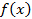, то 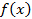делится без остатка на двучлен 
х – .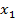
Определение. Наибольшая степень k такая, что многочлен 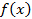делится без остатка на 
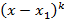, называется кратностью корня х1.
Дата добавления: 2016-10-17; просмотров: 2688;