u(t) называют оригиналом, а функцию U(p) его изображением
Для примера определим изображение функции включения σ(t)=1(t)
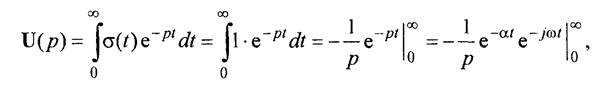
Учитывая
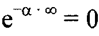
Получим
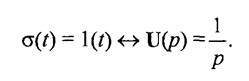
Преобразование Лапласа обладает линейными свойствами, т.е.
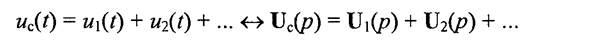
Обратное преобразование Лапласа
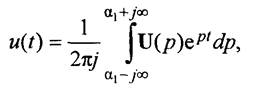
где а1 — вещественная переменная, отражаемая на комплексной плоскости.
Осуществив преобразование Лапласа обеих частей дифференциального уравнения (1), получим
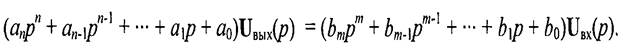
Передаточной функцией (операторным коэффициентом передачи) линейной цепи называется .
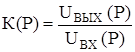
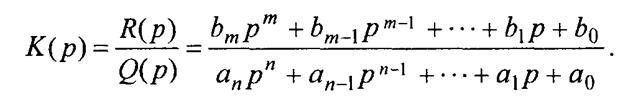
Где через Q(p) обозначают сомножитель перед UВЫХ(р) называя собственным оператором системы, а сомножитель перед UВХ(р) — через R(p) и называют оператором воздействия.
Передаточная функция К(р) отражает результат аналитического переноса комплексного частотного коэффициента передачи К(ω) с мнимой осную на всю область комплексных частот р=α+jω.
Если известна передаточная функция К(р), то выходную реакцию электрической цепи на заданное входное воздействие UВХ(t) можно определить по следующей схеме:
• записать изображение входного сигнала UВХ(t) -> UВХ(р);
• найти изображение выходного сигнала UВЫХ(р) = K(p)* UВХ(р);
• вычислить выходной сигнал UВЫХ(р) -> UВЫХ(t).
Метод интеграла наложения. Cвойства линейных четырехполюсников часто проще оценить видом их отклика на воздействие ряда элементарных сигналов. В качестве элементарных сигналов используются
· прямоугольные импульсы, длительностью ∆, в пределе стремящиеся к дельта-функции δ(t);
· ступенчатые функции, возникающие в виде функций включения σ(t) через равные промежутки времени ∆. Высота каждой ступеньки равна приращению сигнала на интервале времени ∆.
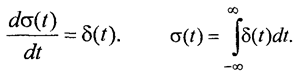 Дельта-функция и функция включения связаны между собой аналитически. Результатом дифференцирования единичной функции является дельта-функция
Дельта-функция и функция включения связаны между собой аналитически. Результатом дифференцирования единичной функции является дельта-функция
Импульсная характеристики линейной цепи h(t) - реакцию системы на поданную на вход дельта-функцию δ(t).
Переходная характеристика g(t) - отклик линейной цепи на единичную функцию σ(t). Пример
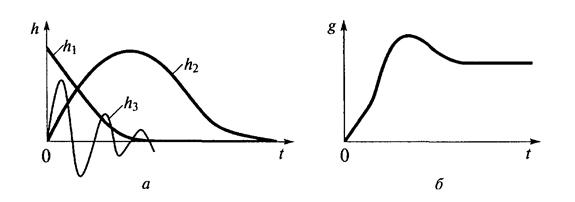
Характеристики линейной цепи.
а — различные виды импульсных; б — переходная
Если входной и выходной сигналы линейной цепи имеют одинаковую размерность, то импульсная характеристика, как и дельта-функция времени, имеет размерность частоты.
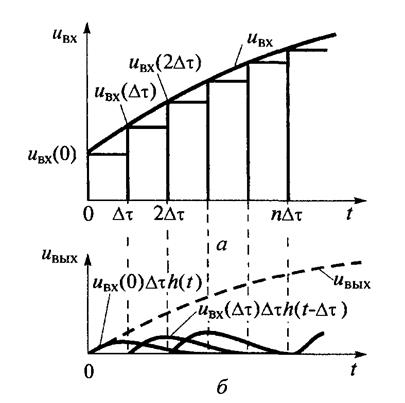
а - входной сигнал- прямоугольных импульсов
б - отклики на импульсы и выходной сигнал
 |
а - входной сигнал- прямоугольных импульсов
б - отклики на импульсы и выходной сигнал
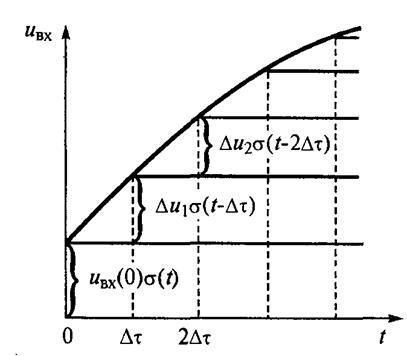
Положим, что требуется определить выходной сигнал UВЫХ(t). Известны ее импульсная характеристика h(t) и входной сигнал UВХ(t). Заменим приближенно кривую входного сигнала UВХ(t)ступенчатой линией в виде совокупности достаточно коротких прямоугольных импульсов, имеющих одинаковую длительность ∆τ. Если выбрать длительность ∆τ бесконечно малой, то отклик линейной цепи на первый по счету прямоугольный импульс будет приближенно равен отклику той же цепи на дельта- функцию (а это будет импульсная характеристика), умноженному на площадь (UВХ(0) ∆τ) первого импульса, т. е. UВХ(0) ∆τ h(t) Откликом цепи на второй импульс является произведение UВХ(∆τ) ∆τ h(t- ∆τ) , где UВХ(∆τ) ∆ τ — площадь этого импульса, а величина h(t- ∆τ) — импульсная характеристика цепи, соответствующая моменту времени t = ∆τ. Следовательно, для некоторого произвольного момента времени t = n ∆τ (n — число условно сформированных импульсов,
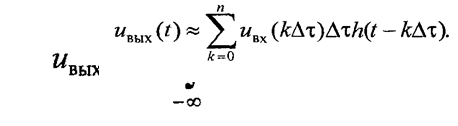 |
приходящихся на интервал времени O...t) отклик линейной цепи приближенно выразится суммой
Если длительность импульсов ∆τ, отражающих входной сигнал, последовательно приближается к нулю, то малое приращение времени ∆τ превращается в dτ, а операция суммирования трансформируется в операцию интегрирования по переменной τ= k ∆τ
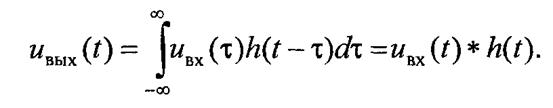 |
В более общей форме
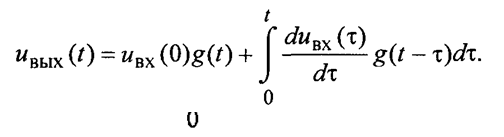 |
В теории электрических цепей часто применяют другую, эквивалентную форму интеграла Дюамеля
 |
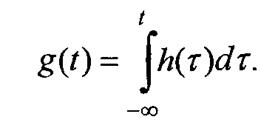
Дата добавления: 2016-06-02; просмотров: 1354;
