Ширина полосы пропускания
∆ω = ωВ - ωН.
Для циклической частоты
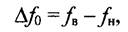 |

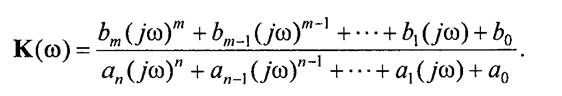 |
Если на вход линейной цепи подается гармонический сигнал единичной амплитуды, имеющий комплексную аналитическую модель вида UВХ(t) = еjωt, то сигнал на ее выходе запишется как UВЫХ(t) = К(ω) еjωt . Подставляя эти выражения в (1), после несложных преобразований запишем К(ω)в форме дифференциального уравнения
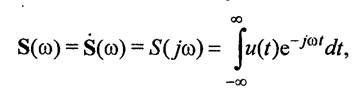 |
Т.е. если коэффициенты постоянные то К(ω)представляет собой дробно-рациональную функцию переменной jω. При этом коэффициенты этой функции совпадают с коэффициентами дифференциального уравнения. С помощью частотного коэффициента передачи К(ω) можно определить сигнал на выходе линейного четырехполюсника. Пусть на входе линейного четырехполюсника с частотным коэффициентом передачи К(ω) действует непрерывный сигнал произвольной формы в виде напряжения UBX(t). Применив прямое преобразование Фурье
определим спектральную плотность входного сигнала SВХ(ω). Тогда спектральная плотность сигнала на выходе линейного четырехполюсника
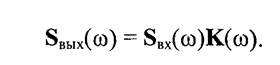
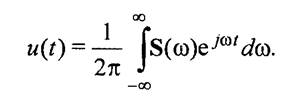 |
Проведя обратное преобразование Фурье
от спектральной плотности, получим выходной сигнал
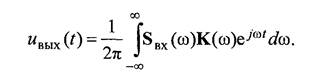
Операторный методоснован на замене оператора дифференцирования d/dt комплексным параметром р, который переводит анализ сигналов из временной области в область комплексных величин. Рассмотрим некоторый комплексный или вещественный аналоговый сигнал u(t), определенный при t≥0 и равный нулю в момент времени t =0. Преобразование Лапласа этого сигнала есть функция комплексной переменной р, выраженная интегралом
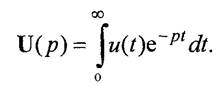
12
Дата добавления: 2016-06-02; просмотров: 811;
