Модель международной торговли (модель обмена)
Данная модель даёт ответ на следующий вопрос: каким должны быть соотношения между государственными бюджетами стран, торгующих между собой, чтобы торговля была взаимовыгодной, т.е. не было значительного дефицита торгового баланса для каждой из стран-участниц? Проблема достаточно важна, т.к. дефицит в торговле между странами порождает такие явления как лицензии, квоты, таможенные пошлины и даже торговые войны.
Для простоты изложения рассмотрим три страны-участницы торговли с госбюджетами Х1, Х2, Х3, которые условно назовем США, Германия и Кувейт. Будем считать, что весь госбюджет каждой страны тратится на закупки товаров либо внутри страны, либо на импорт из других стран. Пусть, скажем, США тратят половину своего бюджета на закупку товара внутри страны, ¼ бюджета – на товары из Германии, оставшиеся ¼ бюджета – на товары из Кувейта. Германия тратит поровну свой бюджет на закупку товаров в США, внутри страны и у Кувейта. Кувейт, в свою очередь, тратит ½ бюджета на закупку товаров у США, ½ бюджета на закупки в Германии и ничего не закупает внутри страны.
Введём структурную матрицу торговли:
C Г К
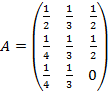 .
.
Заметим, что сумма элементов матрицы А в каждом столбце равна единице.
Пусть 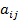 – часть госбюджета, которую j-я страна тратит на закупки товаров i-й страны. После подведения итогов торговли за год страна под номером i получит выручку
– часть госбюджета, которую j-я страна тратит на закупки товаров i-й страны. После подведения итогов торговли за год страна под номером i получит выручку
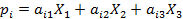 .
.
Например, США получат выручку
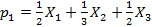 .
.
доля США доля Германии доля Кувейта
Для того, чтобы торговля была сбалансированной, необходимо потребовать бездефицитность торговли для каждой страны:
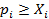 для всех i. (7.1)
для всех i. (7.1)
Предложение. Условием бездефицитности торговли являются равенства
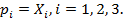 (7.2)
(7.2)
Доказательство. Предположим, что 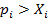 для некоторого i, например, для i = 1. Запишем условие (7.1) для всех i:
для некоторого i, например, для i = 1. Запишем условие (7.1) для всех i:
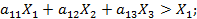
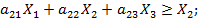
 .
.
Сложив все эти неравенства, имеем:
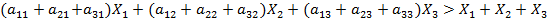 .
.
Поскольку все суммы в скобках левой части неравенства равны 1, то получим противоречивое неравенство
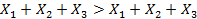 .
.
Следовательно, наше предположение о том, что 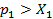 , неверно. Доказательство завершено.
, неверно. Доказательство завершено.
В матричной форме (7.2) выглядит 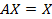 , где
, где 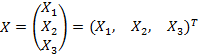 .
.
Дата добавления: 2016-10-17; просмотров: 845;
