Теорема 1 (Фробениуса-Перрона)

1. λ_А – действительное неотрицательное число. Существует неотрицательный собственный вектор 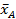, соответствующий данному собственному значению.

2. Если А > 0, то λ_А > 0 и существует положительный собственный вектор.

Определение.Максимальное по модулю собственное значение λ_А неотрицательной матрицы А называется числом Фробениусаматрицы А, а соответствующий ему неотрицательный собственный вектор 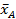– вектором Фробениуса для А.

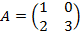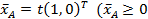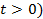Пример.Пусть . У данной неотрицательной матрицы два собственных значения: λ_А=3 – число Фробениуса с собственным вектором при и собственное значение λ₂= 1, которому соответствует собственный вектор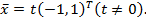

Следствие.Положительный собственный вектор 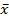неотрицательной матрицы А является её вектором Фробениуса.

Следствие.Вектор Фробениуса положительной матрицы определен однозначно с точностью до умножения на положительное число.

Обозначим через 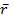- вектор-столбец, координата 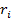которого есть сумма элементов i –й строки матрицы А, а через 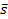- вектор-строку, координата 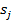которого есть сумма элементов j-го столбца матрицы А. Рассмотрим также вектор-столбец 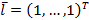, состоящий из одних единиц. Тогда выполняются соотношения

.

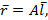
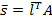Обозначим также

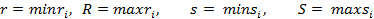
Таким образом, выполняется теорема.

Теорема 2. Число Фробениуса 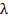_А неотрицательной матрицы А удовлетворяет неравенствам

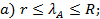
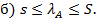
Если к тому же матрица А положительна, то все неравенства строгие, за исключением случая, когда 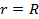или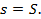

Следствие.Если все суммы строк (столбцов) неотрицательной матрицы А равны одному и тому же числу λ (R = r = λ или 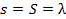), то число Фробениуса 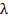_А равно .

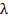Пример. Для матриц

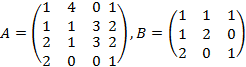
имеем 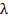_А = 6 (т.к. суммы по столбцам равны 6) и 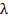_В = 3 (суммы по строкам равны 3).

Балансовые модели