Тема 8. Линейное программирование
Примеры экономико-математических моделей, приводящих к задачам линейного программирования
Рассмотрим математические модели некоторых важных экономических задач.
Задача о банке.
Пусть собственные средства банка в сумме с депозитами составляют 100 млн долл. Часть этих средств, но не менее 35 млн долл., должна быть размещена в кредитах. Кредиты являются неликвидными активами банка, т.к. в случае непредвиденной потребности в наличности обратить кредиты в деньги без существенных потерь невозможно.
Другое дело ценные бумаги (особенно государственные). Их можно в любой момент продать, получив некоторую прибыль, или, во всяком случае, без большого убытка. Поэтому существует правило, согласно которому коммерческие банки должны покупать в определённой пропорции ликвидные активы – ценные бумаги, чтобы компенсировать неликвидность кредитов. В нашем примере ограничение таково: ценные бумаги должны составлять не менее 30% средств, размещённых в кредитах и ценных бумагах.
Пусть х – средства (млн долл.), размещённые в кредитах, у – средства, вложенные в ценные бумаги. Имеем следующую систему ограничений:
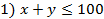 – балансовое ограничение;
– балансовое ограничение;
 – кредитное ограничение;
– кредитное ограничение;
 – ликвидное ограничение;
– ликвидное ограничение;
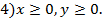
Цель банка состоит в том, чтобы получить максимальную прибыль от кредитов и ценных бумаг:
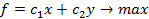 при условии 1)-4),
при условии 1)-4),
где 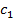 – доходность кредитов,
– доходность кредитов, 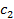 – доходность ценных бумаг.
– доходность ценных бумаг.
Т.к. кредиты менее ликвидны, чем ценные бумаги, то обычно 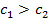 . Мы пришли к задаче линейного программирования с ограничениями 1)-4) и целевой функцией
. Мы пришли к задаче линейного программирования с ограничениями 1)-4) и целевой функцией 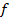 , которую требуется максимизировать.
, которую требуется максимизировать.
Задача об использовании ресурсов (задача планирования производства)
Для производства 2-х видов продукции Р1 и Р2 используют 4 вида ресурсов r1, r2, r3 и r4. Запасы ресурсов и их расход для изготовления единицы продукции каждого вида приведены в таблице:
| Вид ресурса | Количество ед. ресурса для изготовления ед. продукции | Запас ресурса | |
| Р1 | Р2 | ||
| r1 | |||
| r2 | |||
| r3 | - | ||
| r4 | - |
Прибыль, получаемая от реализации единицы продукции Р1 и Р2, равна соответственно 2 и 3 ден. ед.
Требуется составить математическую модель задачи с целью найти такой план производства продукции, при котором прибыль от ее реализации будет наибольшей.
Решение.
Для построения математической модели:
1. Введем управляющие переменные.
Обозначим x1 – количество единиц продукции Р1,
x2 – количество единиц продукции Р2.
По смыслу задачи переменные неотрицательны: x1 ≥0, x2 ≥0,
2. Построим функцию цели.
Прибыль от реализации продукции Р1 составит 2x1 ден. ед., прибыль от реализации продукции Р2 составит 3x2 ден. ед.
Функция цели - суммарная прибыль - должна быть максимальной и описывается выражением: F=2x1 +3x2 → max
3. Построим систему функциональных ограничений.
Расход каждого ресурса для изготовления продукции Р1 и Р2 в количестве x1 и x2 соответственно описывается выражением:
ресурса r1 - 1x1 +3x2
ресурса r2 - 2x1 +1x2
ресурса r3 - 0x1 +1x2
ресурса r4 - 3x1 +0x2
Потребление ресурсов не должно превышать их запасов, поэтому связь между потреблением и запасами ресурсов выразится системой неравенств:
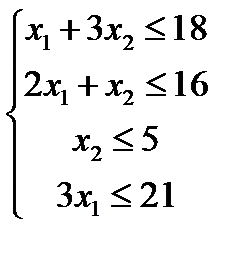
Таким образом, математическая модель задачи построена:
Найти такой план выпуска продукции 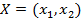 ,
,
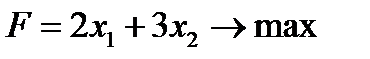 при котором прибыль максимальна
при котором прибыль максимальна
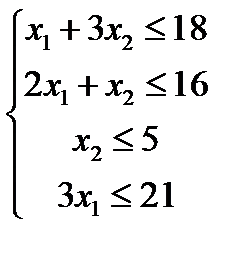 и выполнены ограничения
и выполнены ограничения
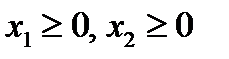
Задача о составлении рациона(о диете, о смесях)
Имеется два вида корма К1 и К2. Данные о содержании витаминов в 1кг каждого вида корма, необходимый минимум этих витаминов и стоимость 1кг каждого вида корма приведены в таблице:
| Витамины | Количество витаминов (ед.)в 1кг корма | Необходимый минимум | |
| К1 | К2 | ||
| А | |||
| В | |||
| С | |||
| Стоимость 1кг корма |
Требуется составить экономико-математическую модель задачи с целью найти дневной рацион, имеющий минимальную стоимость и содержащий не менее установленного предела каждого вида питательных веществ.
Решение.
1. Введем управляющие переменные:
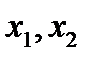 Обозначим - количество кормов К1 и К2, входящих в дневной рацион.
Обозначим - количество кормов К1 и К2, входящих в дневной рацион.
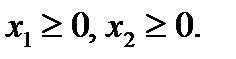 По смыслу переменные неотрицательны:
По смыслу переменные неотрицательны:
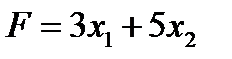
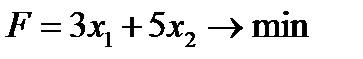 2. Функция цели - общая стоимость дневного рациона питания – описывается выражением и должна быть минимальной:
2. Функция цели - общая стоимость дневного рациона питания – описывается выражением и должна быть минимальной:
3. Построим систему ограничений.
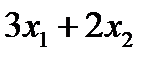 Рацион будет включать следующие количества витаминов:
Рацион будет включать следующие количества витаминов:
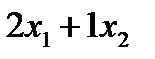 единиц витамина А,
единиц витамина А,
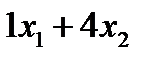 единиц витамина В,
единиц витамина В,
единиц витамина С.
Учитывая установленные пределы содержания питательных веществ, получим систему неравенств:
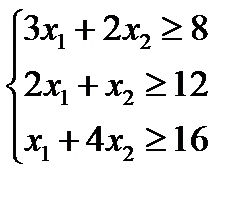
Таким образом, математическая модель задачи получена:
Составить дневной рацион 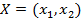 ,стоимость которого минимальна
,стоимость которого минимальна
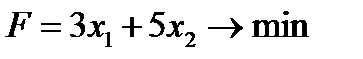
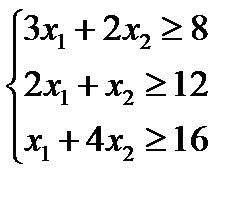 и выполнены заданные ограничения
и выполнены заданные ограничения
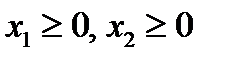
Дата добавления: 2016-10-17; просмотров: 3336;
