Требуется решить задачу
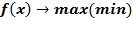 при условии S.
при условии S.
Обычно система S включает в себя условия неотрицательности всех переменных:
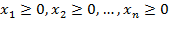 .
.
Будем называть эти условия тривиальными ограничениями.
Каноническая задача линейного программирования.В этом случае система ограничений, помимо тривиальных ограничений, включает в себя только уравнения. Например, последний пример транспортной задачи.
Стандартная задача линейного программирования.Это означает, что система ограничений состоит только из неравенств, в число которых входят и тривиальные ограничения. Примерами могут служить задача о банке, о диете и об использовании ресурсов.
Две разновидности записей ЗЛП сводятся одна к другой. Покажем, как свести стандартную задачу к канонической.
Пусть дана стандартная ЗЛП – будем называть её задачей А:
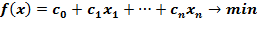 при условиях S.
при условиях S.
Пусть т – число нетривиальных неравенств в системе S. Рассмотрим любое из этих неравенств:
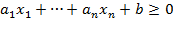 .
.
Введём новую дополнительную переменную 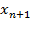 и заменим это неравенство двумя ограничениями: уравнением
и заменим это неравенство двумя ограничениями: уравнением
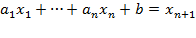
и условием 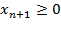 .
.
Если подобную замену произвести с каждым из нетривиальных неравенств системы S, то получим новую систему S1 , состоящую из уравнений, а также условий неотрицательности всех переменных: исходных 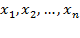 и дополнительных
и дополнительных 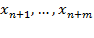 . Дополнительные переменные называют балансовыми.
. Дополнительные переменные называют балансовыми.
Назовём задачей В задачу 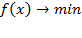 при условиях S1.
при условиях S1.
Сравнивая задачи А и В, нетрудно убедиться в их эквивалентности: любое оптимальное решение задачи А даёт оптимальное решение задачи В, если к значениям переменных 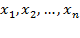 добавить значения балансовых переменных. Обратно, любое оптимальное решение задачи В, если отбросить значения балансовых переменных, даёт оптимальное решение задачи А.
добавить значения балансовых переменных. Обратно, любое оптимальное решение задачи В, если отбросить значения балансовых переменных, даёт оптимальное решение задачи А.
Дата добавления: 2016-10-17; просмотров: 1055;
