Исходная задача Двойственная задача

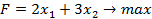
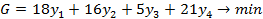
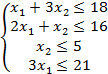
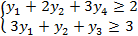
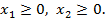
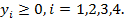
Известно: 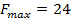при .

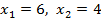Найти .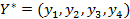

Решение. Проанализируем соотношения теоремы 2.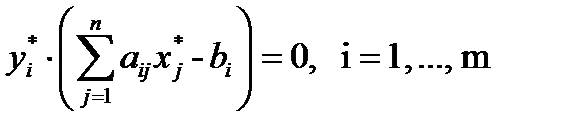

Значит

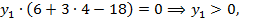
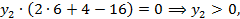
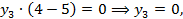
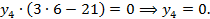
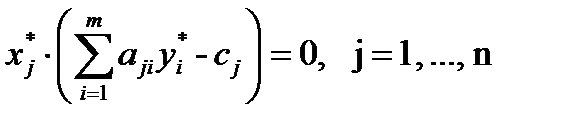
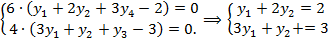
Решая эту систему уравнений, найдём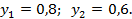

Таким образом, решение двойственной задачи: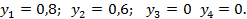

Вычислим значение целевой функции двойственной задачи

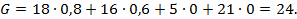
Условие теоремы 1выполнено: 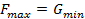=24.

Использование программы «Поиск решения» для экономического анализа

Получить всю необходимую для экономического анализа информацию можно с помощью программы «Поиск решения». Для этого нужно указать тип отчёта – «устойчивость».

Рассмотрим отчёт по устойчивости для задачи об использовании ресурсов:

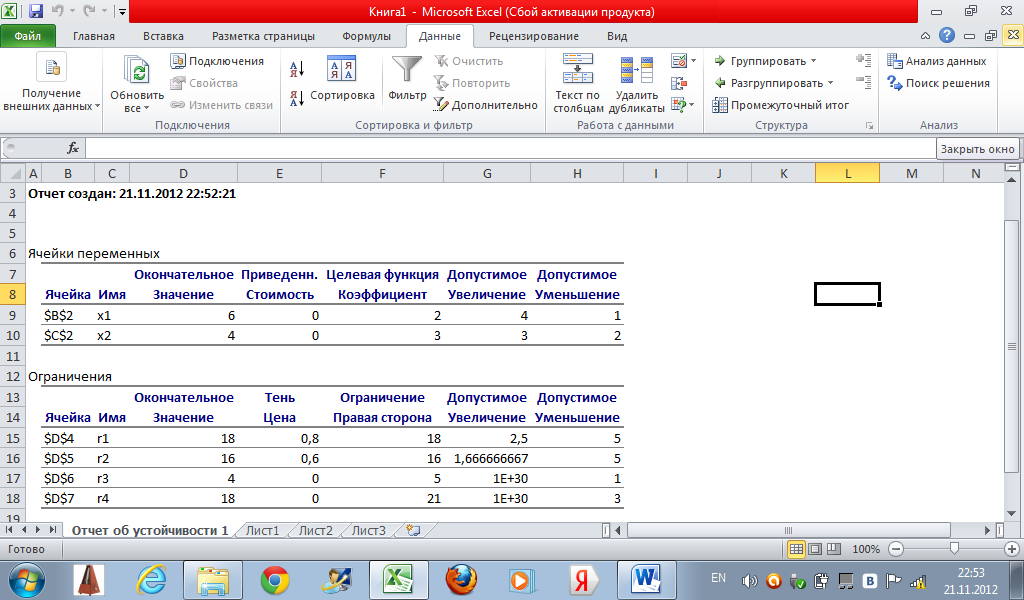
Верхняя часть таблицы содержит информацию, относящуюся к переменным.

· «результ. значение» - найденные оптимальные значения .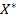

· «нормир. стоимость» - непроизводительные затраты. Для рентабельных видов продукции они равны нулю. Для нерентабельных величина нормированной стоимости показывает, на сколько изменится целевая функция в случае принудительного включения такой продукции в план производства.

· «целевой коэффициент» - коэффициенты целевой функции.

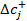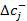· «допустимое увеличение» и «допустимое уменьшение» - предельные значения приращений целевых коэффициентов и , при которых сохраняется оптимальный план прямой задачи.

В рассматриваемой задаче продукт П₁ включен в оптимальный план и для него 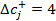и 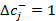. Это означает, что если цена понизится более чем на 1 у.е., или повысится более чем на 4 у.е., то может измениться структура оптимального решения 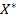и продукт П₁ может стать нерентабельным. Если цена П₁ будет изменяться в интервале устойчивости продукта П₁ 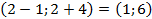, то этот продукт останется рентабельным.

Во второй части таблицы содержится информация, относящаяся к ограничениям.

· «результ. значение» - величина затрат соответствующего ресурса при реализации оптимального плана.

· «теневая цена» - оптимальные значения двойственных переменных .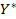

· «ограничения правая часть» - запасы ресурсов.

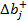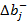· «допустимое увеличение» и «допустимое уменьшение» - предельные значения приращений ресурсов и , при которых сохраняется оптимальный план двойственной задачи.

В рассматриваемой задаче ресурс 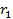является дефицитным и для него 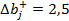и 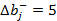. Это значит, что если ресурс 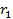увеличится более чем на 2,5 ед. или уменьшится более чем на 5 ед., то может измениться структура оптимального плана 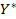и ресурс 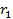может стать недефицитным. Ресурс 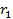останется дефицитным, если его запасы будут изменяться в пределах .

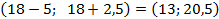Ресурс 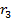останется недефицитным, если его запас будет не менее 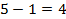единиц (увеличение этого ресурса не влияет на оптимальное решение, что соответствует .

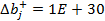Литература

1. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. – М: Финансы и статистика, ИНФРА-М, 2011, ч. 1.

2. Кремер Н.Ш., Фридман М.Н. Линейная алгебра. Учебник и практикум / под ред. Н.Ш. Кремера.– М.: Юрайт, 2014.

3. Высшая математика для экономического бакалавриата. Учебник и практикум / под ред. Н.Ш. Кремера.– М.: Юрайт, 2014.