Рассмотрим пример графического решения ЗЛП по заданной математической модели
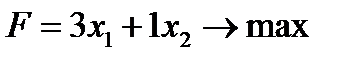Найти
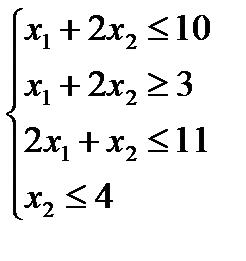при ограничениях
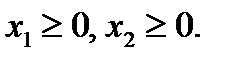
Решение.
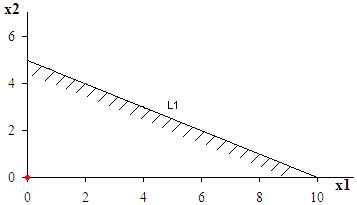
1. Построим область допустимых решений
Ограничения x1 ≥0, x2 ≥0, задают первую координатную четверть плоскости
x1 O x2. Определим полуплоскость, соответствующую каждому неравенству.
Неравенство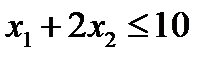 
определяет полуплоскость, ограниченную прямой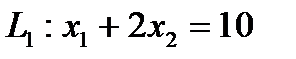 
Она проходит через точки (0; 5) и (10; 0).
В качестве контрольной точки возьмем О (0;0), т.е. x1 = 0, x2 = 0 и подставим ее координаты в правую часть неравенства:
0 ≤ 10 - истина, значит искомая полуплоскость находится с той же стороны, что и точка.
Аналогично построим другие полуплоскости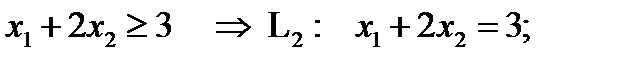 
Возьмем КТ О(0;0):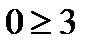 
- ложь, значит, искомая полуплоскость лежит с противоположной стороны от прямой.
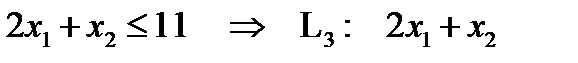=11.
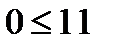Возьмем КТ О(0;0): - истина, значит, искомая полуплоскость находится с той же стороны, что и КТ.
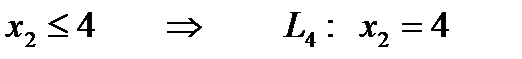
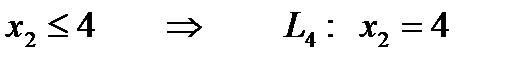
Возьмем КТ О(0;0):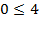 
- истина, значит, искомая полуплоскость находится с той же стороны, что и КТ.
Пересечение всех найденных полуплоскостей определяет область допустимых решений D задачи.
2. Построим линию уровня
Линия уровня определяется уравнением La: F(x1, x2)=a.
Возьмем a = 7 , чтобы линия уровня La: 3x1+1x2 =7 пересекала ОДР.Она проходит через точки с координатами (1;4) и (0;7).
3. Построим вектор градиент
Координаты вектора определяются коэффициентами целевой функции F=3x1+1x2
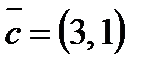
Начало вектора находится в точке (0;0), а точка с координатами (3;1) является концом вектора.
Дата добавления: 2016-10-17; просмотров: 632;