Правила составления двойственных задач
1. Если прямая задача – на максимум, то двойственная к ней – на минимум.
2. Число переменныхв двойственной задаче равно числу ограничений исходной задачи; число ограниченийв двойственной задаче – числу переменных в исходной.
3. Все переменные неотрицательны.
4. В задаче на максимум все неравенства-ограничения имеют вид « ≤ », в задаче на минимум – вид « ≥ ».
5. Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены системы ограничений исходной задачи; правыми частями в ограничениях двойственной задачи – коэффициенты при неизвестных в целевой функции исходной.
6. Матрицы ограничений исходной и двойственной задач являются транспонированными друг к другу.
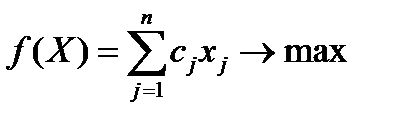 Исходная задача Двойственная задача
Исходная задача Двойственная задача
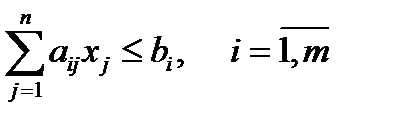
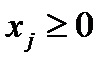
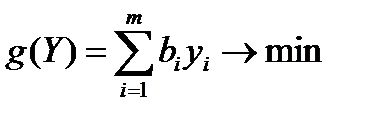
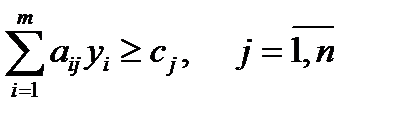
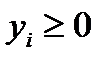
Пример (к задаче об использовании ресурсов).
Построить двойственную задачу к исходной, заданной моделью:
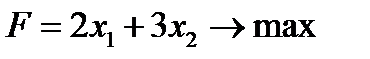
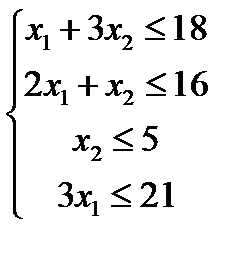
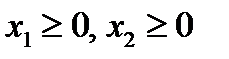
Решение.
Согласно правилам составления двойственной задачи:
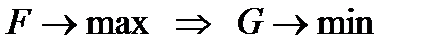 1.
1.
2. В двойственной задаче число переменных – 4; число ограничений – 2.
3. Все переменные y1, y2, y3, y4 неотрицательны.
4. В исходной задаче знак ≤ в двойственной задаче – знак ≥
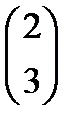 5. Коэффициенты при неизвестных в целевой функции двойственной задачи: (18;16;5;21)
5. Коэффициенты при неизвестных в целевой функции двойственной задачи: (18;16;5;21)
Правые частями в ограничениях двойственной задачи:
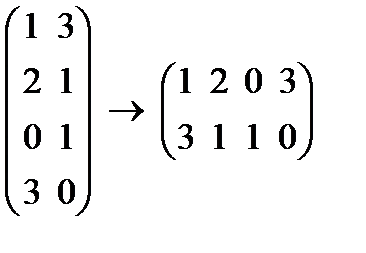 6. Матрицы ограничений исходной и двойственной задач являются транспонированными друг к другу:
6. Матрицы ограничений исходной и двойственной задач являются транспонированными друг к другу:
Вывод: математическая модель двойственной задачи имеет вид:
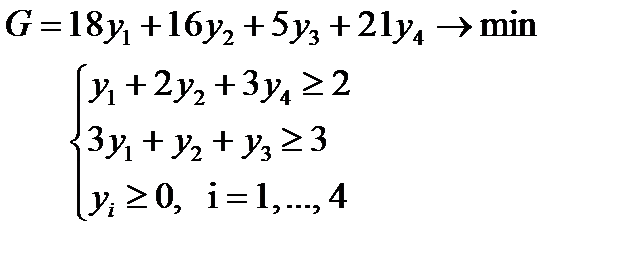
Дата добавления: 2016-10-17; просмотров: 1119;
