Симплекс-метод решения задач линейного программирования
Симплексный метод – это аналитический метод решения ЗЛП, реализующий алгоритм графического метода аналитически, без построения чертежа.
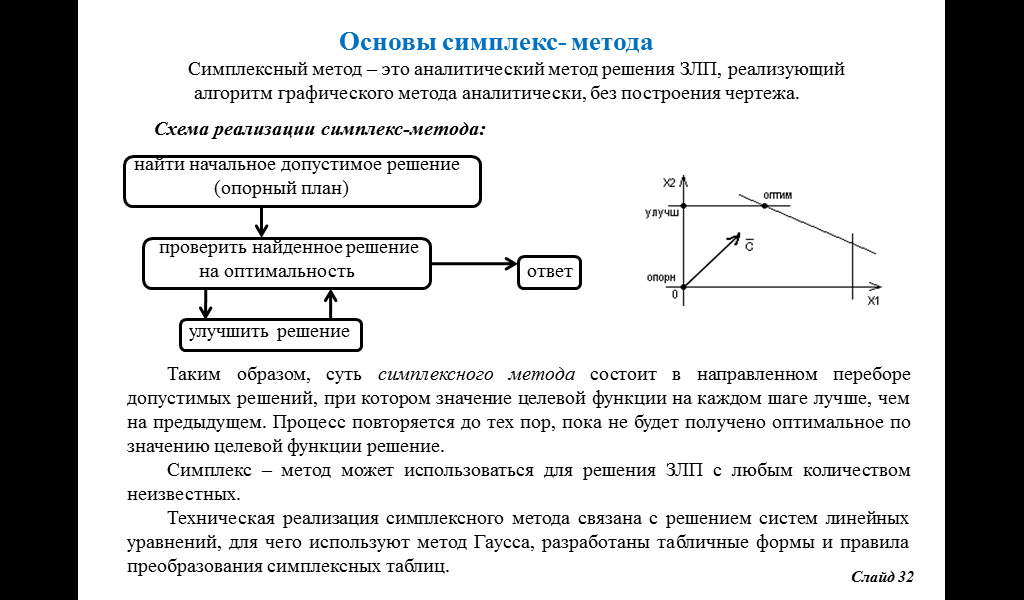
Таким образом, суть симплексного метода состоит в направленном переборе допустимых решений, при котором значение целевой функции на каждом шаге лучше, чем на предыдущем. Процесс повторяется до тех пор, пока не будет получено оптимальное по значению целевой функции решение.
Симплекс метод может использоваться для решения ЗЛП с любым количеством неизвестных.
Техническая реализация симплексного метода связана с решением систем линейных уравнений, для чего используют метод Гаусса, разработаны табличные формы и правила преобразования симплексных таблиц.
Симплекс-метод с естественным базисом применяется, если ЗЛП задана в канонической форме записи, и матрица в КЗЛП содержит единичную подматрицу размером m´m. Для определённости положим, что первые m векторов матрицы системы уравнений составляют единичную матрицу. Тогда первоначальный план выбирается следующим образом:
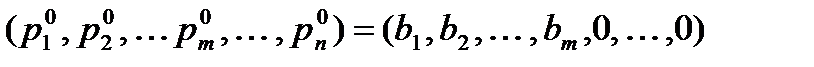 .
.
Проверка на оптимальность опорного плана проходит с помощью признака оптимальности, переход к другому плану проводится с помощью преобразования Жордана-Гаусса при использовании математического признака оптимальности. Полученный опорный план снова проверяется на оптимальность и т.д.
Математический признак оптимальности состоит из следующих двух теорем:
1. Если для всех векторов A1, A2, … , An выполняется условие 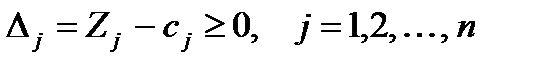 , где
, где 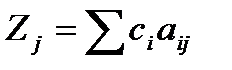 , то полученный опорный план является оптимальным. В сумме для определения Zj участвуют m слагаемых, то есть в ней участвуют не все коэффициенты целевой функции cj, а лишь с номерами соответствующими номерам текущих базисных векторов Ai, количество которых равно m .
, то полученный опорный план является оптимальным. В сумме для определения Zj участвуют m слагаемых, то есть в ней участвуют не все коэффициенты целевой функции cj, а лишь с номерами соответствующими номерам текущих базисных векторов Ai, количество которых равно m .
2. Если для некоторого вектора, не входящего в базис, выполняется условие 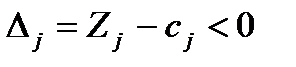 , то следует искать новый опорный план, для которого значение ЦФ больше, чем для текущего. При этом возможны два случая:
, то следует искать новый опорный план, для которого значение ЦФ больше, чем для текущего. При этом возможны два случая:
а) если все компоненты вектора Ak, подлежащего вводу в базис, неположительны, то ЗЛП не имеет решения (конечного оптимума нет);
б) если имеется хотя бы одна положительная компонента у вектора Ak, подлежащего ввода в базис, то можно получить новый опорный план.
На основании признака оптимальности в базис вводится вектор Ak, давший минимальную отрицательную величину симплекс-разности:
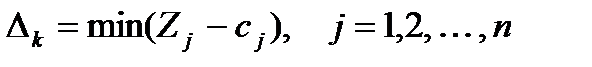 . (8.4)
. (8.4)
Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор Ar, который даёт минимальное положительное оценочное отношение
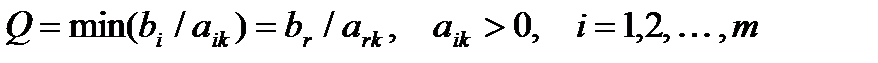 . (8.5)
. (8.5)
Строка Ar, в которой находился старый базисный вектор, называется направляющей, столбец Ak и элемент ark - направляющими.
Элементы направляющей строки в новой симплекс-таблице вычисляются по формулам:
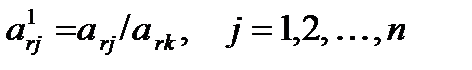 , (8.6)
, (8.6)
а элементы любой другой i-й строки - по формулам:
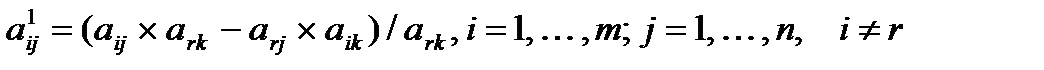 (8.7)
(8.7)
Значения нового опорного плана рассчитываются по аналогичным формулам:
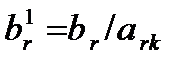 ,
,
для
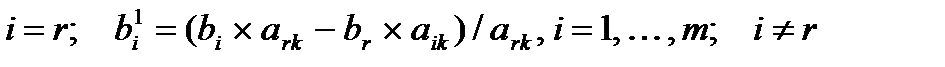 . (8.8)
. (8.8)
Процесс продолжают либо до получения оптимального плана, либо до установления неограниченности ЦФ. Если среди разностей Δj, j=1, 2, … , n оптимального плана нулевыми являются только разности, соответствующие базисным векторам, то это говорит о единственности оптимального плана. Если же нулевая оценка соответствует вектору, не входящему в базис, то в общем случае это означает, что оптимальный план не единственный.
Пример. Решить ЗЛП по модели:
найти 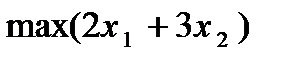 ,
,
при ограничениях 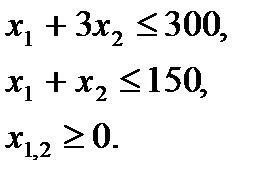
Эта ЗЛП сводится к каноническому виду путём введения дополнительных переменных x3 и x4:
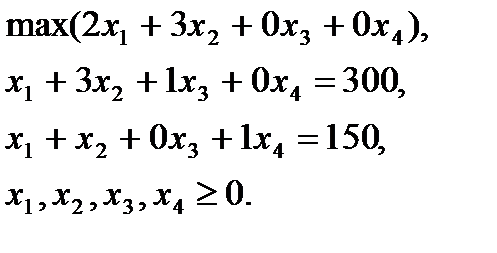
КЗЛП имеет необходимое количество (два) нулевых столбцов при x3 и x4, то есть обладает очевидным начальным опорным планом (0,0,300,150).
Решение осуществляется симплекс-методом с естественным базисом с оформлением расчётов в симплекс-таблицах:
| Номер симплекс-таблицы | Базис | сj | сj | Q | ||||
| B | A1 | A2 | A3 | A4 | ||||
| ← A3 | ||||||||
| A4 | ||||||||
| Δ | - | -2 | -3 | - | ||||
| I | → A2 | 1/3 | 1/3 | |||||
| ← A4 | 2/3 | -1/3 | ||||||
| Δ | - | -1 | - | |||||
| II | A2 | 1/2 | -1/2 | - | ||||
| → A1 | -1/2 | 3/2 | - | |||||
| Δ | - | 1/2 | 3/2 | - |
Остановимся подробнее на заполнении симплекс-таблиц и, соответственно, получении решения КЗЛП.
В верхнюю строку общей таблицы внесены коэффициенты cj, j=1, 2, 3, 4 при переменных в ЦФ. В первые две строки нулевой симплекс-таблицы внесены вектор-столбцы B, A1, A2, A3, A4, соответствующие векторной форме записи КЗЛП. Поскольку исходным базисом является пара векторов A3, A4, они внесены в колонку под названием “Базис” нулевой симплекс-таблицы. При этом, A3 внесён в первую строку, что определяется единицей, являющейся первым элементов этого вектора, а вектор A4 - во вторую строку, у этого вектора единица находится во второй строке. В столбец под названием “ ci ” внесены коэффициенты целевой функции, соответствующие базисным векторам A3, A4, то есть c3, c4. Они оба равны нулю. Далее вычисляются значения разностей Δ для векторов B, A1, A2, A3, A4 и заносятся в третью строку нулевой таблицы. Для вектора A1:
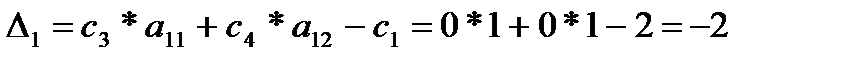 ,
,
для вектора  :
:
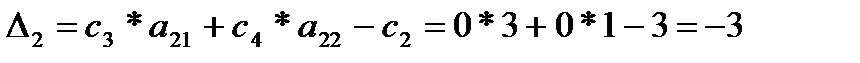 .
.
Аналогично 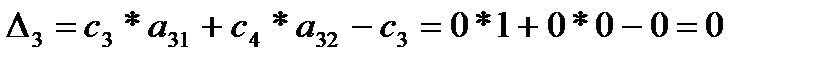 ,
,  .
.
Для вектора B вычисление разности несколько упрощается, поскольку ему нет соответствующего коэффициента cj, j=1, 2, 3, 4 в ЦФ:
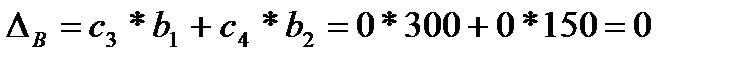 .
.
Не для всех векторов A1, A2, A3, A4 полученные разности являются неотрицательными, поэтому выбранный нами опорный план не является оптимальным. Нам необходимо искать новый опорный план, а для этого нужно заменить один из входящих в базис векторов A3, A4.
Для определения вектора, который мы должны ввести, ищем вектор, для которого значение разности получилось минимальным. Таким является вектор, A2, ему соответствует минимальное значение разности: -3. То есть индекс k из формулы (8.4) равен 2. Для определения вектора, который мы должны будем вывести из базиса, вычисляем значения Q для каждой строки по формуле (8.5) и вносим их в последнюю колонку. В данном случае в каждой строке мы должны величину элемента вектора B разделить на величину элемента вектора A2. В первой строке получим 300/3=100, во второй: 150/1=150. Меньше получилось отношение в первой строке, ей соответствовал базисный вектор A3, следовательно, индекс r в формуле (8.5) равен 1, ark =3 (выделен в таблице рамкой), а выводить из базиса мы будем вектор A3 (обозначено в таблице стрелкой).
Поскольку среди элементов вектора A2, который должен быть введён в базис, имеются положительные, то можно получить новый опорный план и решение следует продолжить.
После этого заполняется вторая симплекс-таблица. Для перерасчёта элементов векторов B, A1, A2, A3, A4 используются формулы (8.6)-(8.8). Они несколько отличаются для определения элементов направляющей строки (в нашем случае первая) и для определения элементов прочих строк. Распишем вычисления нескольких элементов:
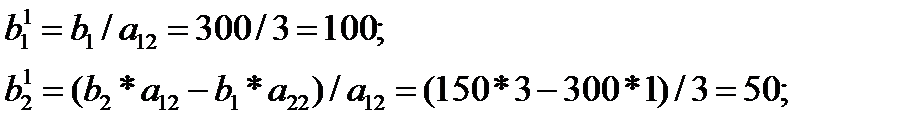
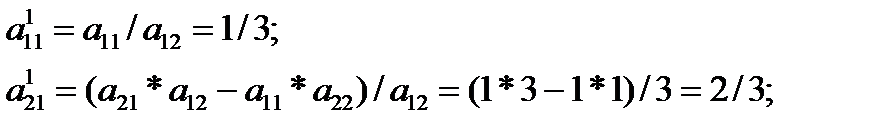
Другие элементы первой симплекс-таблицы вычисляются аналогично тому, как мы это делали для нулевой таблицы. Поскольку не все разности в первой симплекс-таблице неотрицательны, возникает необходимость продолжить расчёты.
Как мы видим, в результате расчётов во второй симплекс-таблице с базисными векторами A2, A1 все разности получились неотрицательные, что означает достижение оптимального плана (75; 75; 0; 0). Симплекс-разность для вектора В равна искомому максимальному значению ЦФ - 375.
Теорема (о конечности симплекс-алгоритма).Если существует оптимальное решение ЗЛП, то существует и базисное оптимальное решение. Последнее всегда может быть получено с помощью симплекс-метода, причём начинать можно с любого исходного базиса.
Дата добавления: 2016-10-17; просмотров: 3075;
