УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПРОРАБОТКИ. Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из определенного количества элементов.
Конспект КОМБИНАТОРИКА
Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из определенного количества элементов.
Формулы комбинаторики часто используют при непосредственном вычислении вероятностей.
Перестановки
Перестановки – комбинации, состоящие из одних и тех же n различных элементов, отличающиеся только порядком их расположения;
обозначаются Pn (перестановки из n элементов)
Число всех возможных перестановок: Pn = n!
| Пример: | Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз? |
| Решение: | P3 = 3! = 1 ´ 2 ´ 3 = 6 |
Размещения
Размещения - комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком;
обозначаются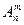 
Число всех возможных комбинаций:
A = n(n-1)(n-2) … (n-m+1)
или
| m A = n | n! | |||
| (n-m)! |
| Пример: | Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2? |
| Решение: | 2 A = 6 | 6! | = | 6! | = 5´6 = 30 |
| (6-2)! | 4! |
Сочетания
Сочетания - комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом;
обозначаются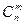 
| m С = n | n! |
| m! (n-m)! |
| Пример: | Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей? |
| Решение: | 2 С = 10 | 10! | = 45 |
| 2!(10-2)! |
| Правило суммы | Если объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m+ nспособами |
| Правило произведения | Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А,В) в указанном порядке может быть выбрана m´nспособами |
Пример.Сколько шестизначных чисел , кратных 5 , можно составить из цифр 1,2,3,4,5,6 при условии, что в числе цифры не повторяются?
Решение. Цифра 5 должна стоять на последнем месте.Остальные пять цифр могут стоять на оставшихся пяти местах в любом порядке.Следовательно,искомое число шестизначных чисел, кратных пяти, равно числу перестановок из пяти элементов ,т.е. 5!=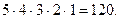 
Пример.Сколько матчей будет сыграно в футбольном чемпионате с участием 16 команд, если каждые две команды встречаются между собой один раз?
Решение. Число матчей равно числу неупорядоченных выборок объема 2 из множества , содержащего 16 элементов , т.е. равно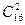 
. По формуле находим
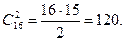
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПРОРАБОТКИ
| 1. | Сколько различных двузначных чисел можно образовать из цифр 1, 2, 3, 4 при условии, что в каждом числе нет одинаковых цифр? | |
| 2. | Сколько различных двузначных чисел можно образовать из цифр 1, 2, 3, 4 ? | |
| 3. | Из цифр 0, 1, 2, 3составлены все возможные 4-х значные числа так, что в каждом числе нет одинаковых цифр. Сколько получилось чисел? | |
| 4. | Сколько различных перестановок можно образовать из букв следующих слов: 1. зебра, 2. баран, 3. водород, 4 абракадабра? | |
| 5. | Сколькими способами можно составить расписание занятий на понедельник, если в этот день должно быть 5 уроков: алгебра, геометрия, история, география, литература, причем, алгебра и геометрия не должны следовать непосредственно друг за другом? | |
| 6. | Сколькими способами можно расположить в ряд 5 белых и 4 черных шара так, чтобы черные шары не лежали рядом? Шары одного цвета не отличимы друг от друга. | |
| 7. | Укротителю диких зверей предстоит вывести на арену цирка одного за другим 5 львов и 4 тигра. Сколькими способами он может это сделать, причем так, чтобы никакие 2 тигра не шли непосредственно друг за другом? | |
| 8. | На 5 сотрудников выделены три путевки. Сколькими способами их можно распределить, если: - все путевки различны; - все путевки одинаковы? | |
| 9. | В группе 30 студентов. Сколькими способами можно выделить двух человек для дежурства, если: - один из них должен быть старшим; - старшего быть не должно? | |
| 10. | В почтовом ящике 38 отделений. Сколькими способами можно положить в ящик 35 одинаковых открыток так, чтобы в каждом отделении было не более одной открытки? | |
| 11. | В розыгрыше первенства по футболу было сыграно 153 матча. Каждые две команды встречались между собой один раз. Сколько команд участвовало в розыгрыше первенства? | |
| 12. | В шахматном турнире, где участники встречаются между собой один раз, два шахматиста выбыли по болезни, успев сыграть только по три партии каждый. Сколько шахматистов начали турнир, если всего было сыграно 84 партии? | |
| 13. | Сколько диагоналей имеет выпуклый десятиугольник? | |
| 14. | Никакие три диагонали выпуклого десятиугольника не пересекаются в одной точке. Определите число точек пересечения диагоналей. | |
| 15. | Во взводе 3 сержанта и 30 солдат. Сколькими способами можно выделить одного сержанта и трех солдат для патрулирования? | |
| 16. | Буквы азбуки Морзе представляют собой набор точек и тире. Сколько букв может быть в азбуке Морзе, если: - буква не должна содержать более четырех знаков; - буква не должна содержать более пяти знаков? | |
ЧАСТЬ ПЕРВАЯ
СЛУЧАЙНЫЕ СОБЫТИЯ
Основные понятия
| Совместные события | - | события, которые могут происходить одновременно |
| Несовместные события | - | исключающие друг друга события |
| Независимые события | - | события, которые могут происходить независимо друг от друга |
Обозначения
| A | - | событие |
| _ a; A | - | событие, противоположное событию А |
| P(A) | - | вероятность наступления события А |
| m | - | число случаев, благоприятствующих событию |
| n | - | общее число случаев |
| AB; (AÇB) | - | совместное осуществление событий А и В |
| (A+B); (AÈB) | - | любое сочетание событий: или А или В или одновременно А и В |
| x | - | Условие |
| P(A/x) | - | условная вероятность (вероятность события А при условии события x |
Дата добавления: 2016-09-20; просмотров: 1922;