ПРЯМОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
| P(A) = | m | - | математическая вероятность наступления события А, определяющаяся из условий проведения испытаний |
| n | |||
| P*(A)= | m | - | статистическая вероятность (частотная), определяющаяся из статистики результатов множества предыдущих испытаний |
| n |
| Вероятность противоположного события: |
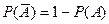
|
Вероятность зависит от наличия информации о событиях, а не от объективной действительности.
Понятие “истинной” вероятности не имеет смысла.
Примеры:
1. Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях четная, причем, на грани хотя бы одной из костей появится шестерка.
Решение
На выпавшей грани первой игральной кости может появиться одно очко, два, три очка … шесть очков. Аналогичные шесть элементарных исходов возможны при бросании второй кости. Каждый из исходов бросания первой кости может сочетаться с каждым из исходов бросания второй кости.
Общее число возможных элементарных исходов равно 6´6=36
Благоприятствующими интересующему нас событию является следующие пять исходов:
| Число выпавших очков | Сумма очков | |
| 1-я кость | 2-я кость | |
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех возможных исходов:
Р=5/36=0,13
2. Набирая номер телефона, абонент забыл две последние цифры и , помня лишь ,что эти цифры различны , набрал их наудачу.Какова вероятность того , что номер набран правильно?
Решение.
Две последние цифры можно набрать 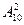 способами, а благоприятствовать событию A будет только один способ.Поэтому
способами, а благоприятствовать событию A будет только один способ.Поэтому 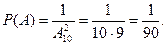
3. Среди 100 электроламп 5 испорченных.Какова вероятность того , что выбранные наудачу 3 лампы окажутся исправными?
Решение.
Из 100 электроламп 3 лампы можно выбрать  способами.Три исправных лампы из общего числа 95 исправных ламп можно выбрать
способами.Три исправных лампы из общего числа 95 исправных ламп можно выбрать 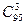 способами. Следовательно , искомая вероятность
способами. Следовательно , искомая вероятность
равна
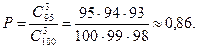
4. В партии из n изделий k бракованных. Определить вероятность того , что среди выбранных наудачу для проверки m изделий ровно l окажутся бракованными.
Решение.
Число возможных способов взять m изделий из n изделий равно 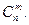 Благоприятствующими являются случаи , когда из общего числа k бракованных изделий взято l , а остальные m-l изделий небракованные , т.е. они взяты из общего числа n-k. Поэтому число длагоприятствующих случаев равно
Благоприятствующими являются случаи , когда из общего числа k бракованных изделий взято l , а остальные m-l изделий небракованные , т.е. они взяты из общего числа n-k. Поэтому число длагоприятствующих случаев равно 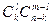 . Искомая вероятность будет
. Искомая вероятность будет
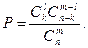
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПРОРАБОТКИ
1. Задумано двузначное число. Найти вероятность того, что задуманным числом окажется:
- случайно названное двузначное число
- случайно названное двузначное число, цифры которого различны
2. Брошены две игральные кости. Найти вероятность следующих событий:
- сумма выпавших очков равна семи
- сумма выпавших очков равна восьми, а разность - четырем
- сумма выпавших очков равна восьми, если известно, что их разность равна четырем
- сумма выпавших очков равна пяти, а произведение - четырем
3. Монета брошена два раза. Найти вероятность того, что хотя бы один раз появится герб
4. В коробке шесть одинаковых, занумерованных кубиков. Наудачу по одному извлекают все кубики. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке
5. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
6. В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная
7. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены четыре детали. Найти вероятность того, что среди извлеченных деталей:
- нет бракованных
- нет годных
8. Устройство состоит из пяти элементов, из которых два изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включенными окажутся неизношенные элементы
10. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры
11. В цехе работают шесть мужчин и четыре женщины. ПО табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины
12. На складе имеется 15 кинескопов, причем, 10 из них изготовлены Львовским заводом. Найти вероятность того, что среди пяти взятых наудачу кинескопов окажутся три кинескопа Львовского завода
13. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников
14. При игре в “спортлото” на специальной карточке отмечаются 6 номеров из 49. Во время тиража определяются 6 выигравших номеров. Какова вероятность угадать ровно 3 “счастливых” номера?
Дата добавления: 2016-09-20; просмотров: 1021;
