Основные теоремы теории вероятностей

Название теоремы	Трактовка теоремы	Обозначения

Теорема сложения вероятностей не-совместных собы-тий	Вероятность наступления одного из 2-х несов-местных событий равна сумме вероятностей этих событий.	P(A+B) = P(A) + P(B)

Теорема умножения вероятностей	Вероятность совместного наступления 2-х независимых событий равна произведению их вероятностей	P(AB) = P(A) * P(B

Название теоремы	Трактовка теоремы	Обозначения

Теорема сложения вероятностей сов-местных событий	Вероятность наступления хотя бы одного из 2-х совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления.	P(A+B)=P(A)+P(B)-Р(АВ) Графически это можно пояснить так:

		100%
Р(А)
	Р(В)

Часть вероятности наступления каждого события совпадает с вероятностью их совместного наступления.

Примеры:

1. Сколько надо бросить игральных костей, чтобы с вероятностью, меньшей 0,3, можно было ожидать, что ни на одной из выпавших граней не появится шесть оков?

Решение

Введем обозначения событий”:

А - ни на одной из выпавших граней не появится 6 очков;

А_i – на выпавшей грани i-той кости (i = 1, 2, 3, … , n) не появится 6 очков.

Интересующее нас событие А состоит в совмещении событий А₁, А₂, А₃, … А_n, т.е. А=А₁ А₂, … А_n.

Вероятность того, что на любой выпавшей грани появится число очков, не равное шести, равна Р(А_i) = 5/6

События А_i независимы в совокупности, поэтому применима теорема умножения:

Р(А) = Р(А₁ А₁, … А_n) = Р(А₁) Р(А₂) … Р(А_n) = (5/6)ⁿ

По условию (5/6)ⁿ < 0,3. Следовательно, n ln(5/6) < ln 0,3.

Отсюда, учитывая, что ln(5/6) < 0, найдем: n>6,6.

Т.о. искомое число игральных костей n ³7.

2. В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете.

Решение

Введем обозначения событий”:

А - первый взятый учебник имеет переплет;

В – второй учебник имеет переплет.

Вероятность того, что первый учебник имеет переплет:

Р(А) = 3/6 = 1/2

Вероятность того, что второй учебник имеет переплет при условии, что первый взятый учебник был в переплете, т.е. условная вероятность события В:

Р_А(В) = 2/5

Искомая вероятность того, что оба учебника имеют переплет, по теореме умножения вероятностей равна:

Р(АВ) = Р(А) Р_А(В) = 1/2 ^. 2/5 = 0,2.

3. Разрыв электрической цепи происходит в том случае , когда выходит из строя хотя бы один из трех последовательно соединенных элементов. Определить вероятность того , что не будет разрыва цепи , если элементы выходят из строя соответственно с вероятностями 0,3 , 0,4 и 0,6. Как изменится искомая вероятность , если первый элемент не выходит из строя?

Решение.

Искомая вероятность равна вероятности того , что не выйдут из строя все три элемента. Пусть событие 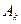означает , что k-й элемент не выйдет из строя (k=1,2,3). Тогда p=P( 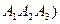. Так как события независимы , то

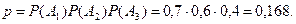
Если первый элемент не выходит из строя , то

<1 2 345 6 7 >

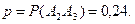
Дата добавления: 2016-09-20; просмотров: 2242;