Геометрические вероятности

Дан отрезок:		L






	l

L - длина отрезка

l - часть отрезка

На отрезок L наугад наносится точка.

Вероятность попадания в отрезок l :

P =	l
L

Дана плоская фигура:


g
		G - площадь всей фигуры
		g - площадь части фигуры
	G

P =	g
G

Аналогично определяется вероятность попадания точки в пространственную фигуру.

P =	v
V

где:	V- объем всей фигуры
	v- объем части фигуры

Пример. На отрезке L=16 см помещен отрезок l=4 см. Найти вероятность того , что наугад поставленная на отрезок L точка попадет в отрезок l.

Решение.

Искомая вероятность равна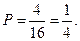

УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПРОРАБОТКИ

1.	На отрезке L = 20 см помещен отрезок l= 10 см. Найти вероятность того, что наугад поставленная на отрезок L точка попадет в отрезок l.

2.	В круге радиусом R есть круг радиуса r. Найти вероятность того, что наугад брошенная в большой круг точка попадет в малый круг.

3.	Плоскость разграфлена параллельными прямыми, находящимися друг от друга на расстоянии 2а. На плоскость наудачу брошена монета радиусом r < a. Найти вероятность того, что монета не пересечет ни одной из прямых.

4.	На плоскость с нанесенной сеткой квадратов со стороной a наудачу брошена монета радиусом r < a/2. Найти вероятность того, что монета не пересечет ни одну из сторон квадрата:

5.	На плоскости начерчены две концентрические окружности с радиусами 5 см и 10 см. Найти вероятность того, что точка, брошенная в большой круг, попадет в кольцо, образованное двумя окружностями.

КОСВЕННОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ

Основные понятия

№№ пп	События	Сущность Событий	Обозначения

1.	Несовместные	Одно из двух	(А+В)

2.	Противоположные		(А+В)

3.	Совместные:
	- независимые	- совместное наступление	(АВ)
		- хотя бы одно из 2-х	А+В


	- зависимые	- совместное наступление	(АВ)

4.	Условная вероятность	вероятность события А при условии события x	P(A/x)

<1 234 5 6 7 >

Дата добавления: 2016-09-20; просмотров: 901;