УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПРОРАБОТКИ
| 1. | Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы (за время t) первого, второго и третьего элементов соответственно равны 0,6; 0,7; 0,8. Найти вероятность того, что за время t безотказно будут работать: - только один элемент - только два элемента - все три элемента |
| 2. | Верояьность попадания в мишень стрелком при одном выстреле равна 0,8. сколько выстрелов должен произвести стрелок, чтобы с вероятностью, меньшей 0,4, можно было ожидать, что не будет ни одного промаха? |
| 3. | Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что 2 наудачу выбранные билета окажутся выигрышными. |
| 4. | В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу отобраны 3 человека. Найти вероятность того, что все отобранные лица окажутся мужчинами. |
| 5. | Из колоды в 36 карт наудачу вынимают одну. Какова вероятность того, что будет вынута пика или туз? |
Вероятность наступления хотя бы одного из множества событий
Вероятность наступления события А, состоящего в наступлении хотя бы одного из событий А1, А2, А2, … Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий:
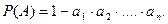
Примеры:
1. В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказов первого, второго и третьего элементов соответственно равны:
Р1=0,1
Р2=0,15
Р3= 0,2
Найти вероятность того, что тока в цепи не будет.
Решение
Элементы включены последовательно, поэтому тока в цепи не будет (событие А), если откажет хотя бы один элемент.
Искомая вероятность:
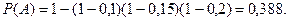
2. Вероятность успешного выполнения упражнения для каждого из двух спортсменов равна 0,5. Спортсмены выполняют упражнение по очереди, причем, каждый делает по две попытки. Выполняющий упражнение первым получает приз.
Найти вероятность получения приза спортсменами.
Решение
Для вручения приза достаточно, чтобы хотя бы одна из четырех попыток была успешной. Вероятность успешной попытки равна Р = 0,5, а неуспешной - 1 – 0,5 = 0,5.
Искомая вероятность равна:
Р =1 – а4 = 0,9375.
3. Вероятность хотя бы одного попадания стрелком в мишень при трех выстрелах равна 0,875.
Найти вероятность попадания при одном выстреле.
Решение
Вероятность попадания в мишень хотя бы при одном из трех выстрелов (событие А) равна:
Р(А) = 1- а3,
где а– вероятность промаха.
По условию Р(А) = 0,975. Следовательно:
0,875 = 1 - а3
иили
а3 = 1 – 0,875 = 0,125
| Отсюда а = | 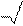 3 3
| 0,125 | = 0,5 |
Вероятность: Р = 1- а = 1 – 0,5 = 0,5
Дата добавления: 2016-09-20; просмотров: 1732;
