УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПРОРАБОТКИ. 1. В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом
| 1. | В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него? |
| 2. | Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина. |
| 3. | Две перфораторщицы набили на разных перфораторах по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустить ошибку, равна 0,05; для второй перфораторщицны эта вероятность равна 0,1. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась первая перфораторщица. (Предполагается, что оба перфоратора исправны). |
| 4. | В специализированную больницу поступают в среднем 50% больных с заболеванием К, 30% - с заболеванием L, 20% - с заболеванием М. Вероятность полного излечения болезни К равна 0,7; для болезней L и М эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием К. |
| 5. | Изделие проверяется на стандартность одним из двух товароведом. Вероятность того, что изделие попадает к первому товароведу, равна 0,55, а ко второму – 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым - 0,98. Стандартное изделие при проверке было признано стандартным. Найти вероятность того, что это изделие проверил второй товаровед. |
Формула Бернулли
Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0<p<1), событие наступит ровно k раз (безразлично, в какой последовательности), равно
Pn (k) = Ckn pk qn-k
или
| Pn (k) = | n! | pk qn-k |
| k! (n-k)! |
где: q = 1 - p
Вероятность того, что в nиспытаниях событие наступит:
| а) менее k раз | Pn (0) + 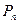 (1) + . . . + Pn (k-1) (1) + . . . + Pn (k-1)
|
| б) более k раз | Pn (k+1) + Pn (k+2) + . . . + Pn (n) |
| в) не менее k раз | Pn (k) + 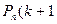 ) + . . . + Pn (n) ) + . . . + Pn (n)
|
| г) не более k раз | Pn (0) + 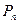 (1) + . . . + Pn (k) (1) + . . . + Pn (k)
|
Примеры:
1. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три партии из шести (ничьи во внимание не принимаются)?
Решение
Вероятность выигрыша у равносильных шахматистов р = 1/2
Вероятность проигрыша q = 1/2
Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли.
Вероятность того, что будут выиграны партии:
| а) две из четырех: | Р4(2) = С24 p2 q2 = 4.3/(1.2) . (1/2)2 . (1/2)2 = 6/16 |
| б) три из шести: | Р6(3) = С36 p3 q3 = 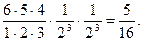
|
Так как Р4(2) > Р6(3), то вероятнее выиграть две партии из четырех
.
2. Найти вероятность того , что при 10- кратном бросании монеты герб выпадет ровно 5 раз.
Решение.
Здесь вероятность выпадения герба при одиночном испытании 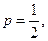 отсюда
отсюда 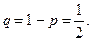
По формуле Бернулли имеем
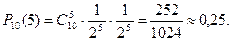
Дата добавления: 2016-09-20; просмотров: 1362;
