УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПРОРАБОТКИ. 1. Устройство содержит два независимо работающих элемента

1.	Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
2.	Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны 0,3; 0,4; 0,6; 0,7
3.	Три исследователя независимо один от другого производят измерения некоторой физической величины. Вероятность того, что первый исследователь допустит ошибку при считывании показаний прибора, равна 0,1. Для второго и третьего исследователей эта вероятность соответственно равна 0,15 и 0,2. Найти вероятность того, что при однократном измерении хотя бы один из исследователей допустит ошибку.
4.	Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый должен сделать по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что стрелки получат приз.
5.	Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.

Формула полной вероятности

Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) В₁, В₂, … В_n, образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:

Р(А) = Р(В₁)^.Р_В1(А) + Р(В₂)^.Р_В2(А) + … + Р(В_n)^.Р_В_n(А)	- формула
	полной вероятности

Где Р(В₁) + Р(В₂) + … + Р(В_n) = 1

Примеры:

1. В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).

Решение

Обозначим: А – извлечен белый шар

В₁- белых шаров первоначально не было

В₂– первоначально был один белый шар

В₃–первоначально было два белых шара

Все три гипотезы равновероятны.. сумма вероятностей гипотез равна единице. Вероятность каждой гипотезы равна:

Условная вероятность извлечения белого шара

Первоначальные условия	Условная вероятность

Белых шаров не было	Р_В1(А) = 1/3

Первоначально был один белый шар	Р_В2(А) = 2/3

Первоначально было два белых шара	Р_В3(А) = 3/3=1

Искомую вероятность того, что будет извлечен белый шар, находим по формуле полной вероятности:

Р(А) = Р(В₁)^.Р_В1(А) + Р(В₂)^.Р_В2(А)+ Р(В₃)^.Р_В3(А) =

= 1/3^.1/3 + 1/3^.2/3 + 1/3^.1 = 2/3.

2. В магазин для продажи поступает продукция трех фабрик , относительные доли которых есть : 1 -50% , 2 – 30% и 3 – 20%. Для продукции фабрик брак соответственно составляет : 1 – 2% , 2 – 3% и 3 – 5%. Какова вероятность того , что изделие этой продукции , случайно приобретенное в магазине , окажется доброкачественным ( событие А).

Решение.

Здесь возможны следующие три гипотезы: приобретенная вещь выработана соответственно на 1, 2, и 3 фабриках ; очевидно , система этих гипотез полная , причем их вероятности

Соответствующие условные вероятности события А равны

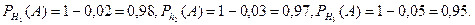
По формуле полной вероятности имеем

<4 567 8 9 10 >

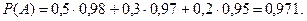
Дата добавления: 2016-09-20; просмотров: 1733;