Методы решения ОДУ.
Обыкновенные дифференциальные уравнения могут быть решены следующими методами:
- аналитическими;
- численными;
- графическими;
- приближенными.
Аналитические методы дают решение в виде аналитического выражения.
Графические методы дают приближенное решение в виде графика.
Численные методы дают частное решение для определенных 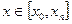 в виде таблицы, Численные методы применяются только к корректно поставленным задачам, т.е. к таким, у которых малое изменение начальных значений, приводит к малому изменению интегральных кривых.
в виде таблицы, Численные методы применяются только к корректно поставленным задачам, т.е. к таким, у которых малое изменение начальных значений, приводит к малому изменению интегральных кривых.
Пример.
Пусть дано следующее ОДУ:
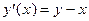 .
.
Необходимо решить задачу Коши для 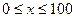 .
.
Начальные условия имеют вид:
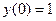
Общее решение имеет вид:
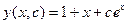
при 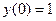
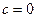 решение
решение 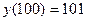 .
.
Однако при малом изменении начальных условий:
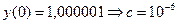 решение в точке
решение в точке 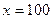 :
: 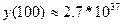 . То есть имеет место плохо обусловленная задача.
. То есть имеет место плохо обусловленная задача.
Численные методы решения обыкновенных дифференциальных уравнений.
Метод Эйлера.
В основе метода Эйлера (метод ломаных) лежит идея графического построения решения дифференциальных уравнений, однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.
Пусть дано дифференциальное уравнение:
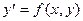
с начальными условиями:
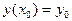 .
.
Выбрав достаточно малый шаг h, строится система равноотстоящих точек 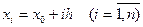 .
.
В методе Эйлера приближенные значения 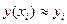 вычисляются последовательно по формулам:
вычисляются последовательно по формулам:
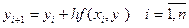 .
.
При этом искомая интегральная кривая 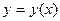 , проходящая через точку
, проходящая через точку 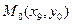 , заменяется ломанной
, заменяется ломанной 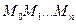 с вершинами
с вершинами 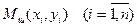 ; каждое звено
; каждое звено 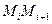 этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения
этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения 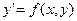 , которая проходит через точку
, которая проходит через точку 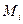

 y
y
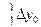
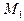
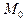
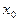
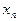
Пример
Пусть дано дифференциальное уравнение:
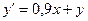
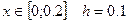
с начальными условиями:
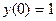 .
.
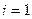
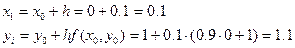
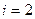
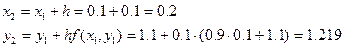
Решение ОДУ имеет вид:
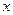
| 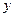
|
| 0.0 | 1.000 |
| 0.1 | 1.100 |
| 0.2 | 1.219 |
Дата добавления: 2016-09-20; просмотров: 1176;
