ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ.

Показательная функция имеет вид:

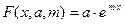
Если прологарифмировать данное уравнение, то можно получить следующее:

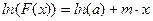
Введя новые переменные:

,

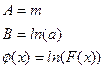получаем следующее линейное уравнение:

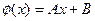
Определив параметры А и В (см. линейную функцию), можно определить параметры степенной функции:

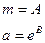
Результаты вычислений лучше всего оформить в виде таблицы

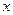
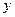
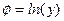
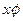
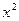
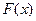
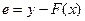
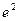
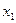
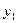
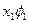
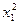
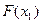
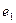
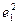
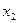
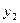
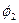
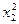
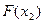
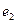
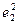
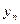
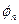
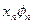
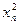
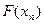
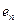
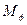
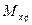
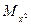
							E

Следует заметить, что данный алгоритм справедлив только для положительных значений y.

ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ.

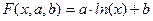
Введя новую переменную:

,

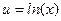получаем следующее линейное уравнение:

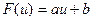
Результаты вычислений лучше всего оформить в виде таблицы

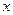
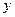
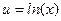
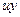
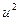
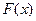
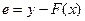
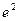
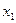
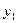
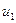
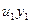
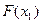
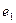
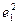
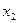
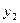
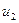
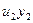
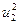
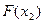
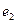
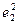
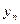
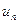
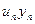
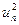
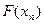
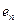
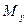
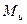
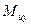
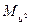
							E

Следует заметить, что данный алгоритм справедлив только для положительных значений u.

ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ.

Преобразуем следующим образом:

Введя новую переменную:

,

получаем следующее линейное уравнение:

Результаты вычислений лучше всего оформить в виде таблицы

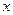
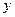
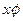
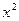
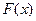
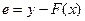
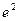
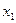
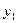
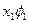
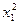
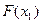
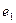
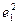
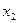
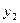
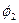
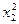
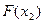
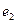
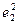
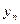
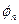
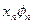
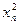
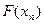
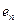
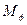
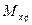
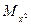
							E

Следует заметить, что данный алгоритм справедлив только для y, отличных от нуля.

ГИПЕРБОЛА.

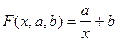
Введя новую переменную:

,

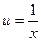получаем следующее линейное уравнение:

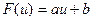
Результаты вычислений лучше всего оформить в виде таблицы

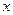
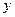
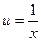
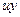
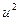
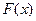
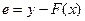
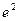
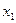
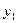
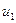
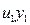
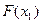
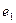
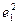
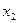
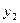
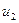
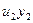
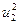
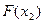
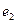
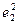
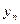
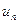
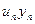
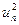
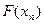
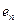
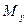
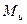
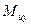
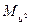
							E