Сходимость метода итераций для решения системы алгебраических уравнений
Теорема: Система уравнений имеет единственное решение и сходится при любом начальном значении 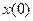 тогда и только тогда, когда все собственные значения матрицы
тогда и только тогда, когда все собственные значения матрицы 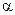 по модулю меньше 1.
по модулю меньше 1.
Если для системы уравнений
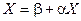
выполнено хотя бы одно из условий:
1. 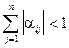 ,
, 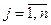
2. 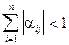 ,
, 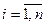
то процесс итерации сходится, независимо от выбора начального условия.
Однако этой теоремой в общем случае очень тяжело воспользоваться, поэтому на практике пользуются другим правилом менее жёстким.
Если эти условия выполняются, то в принципе логично выбрать для начальных значений. На практике в качестве начального приближения используют вектор свободных членов.
Приведение линейной системы к виду, удобному для итерациию.
Теорема сходимости накладывает жёсткие условия к коэффициентам данной линейной системы.
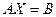
Однако, если 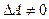 , то эту систему всегда можно привести к такому виду:
, то эту систему всегда можно привести к такому виду:
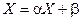 , чтобы удовлетворить условиям 1
, чтобы удовлетворить условиям 1
Первый способ.
Дано: 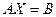
Домножим это уравнение на матрицу 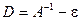 , где
, где 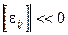
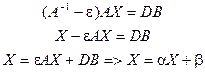 ,
,
где 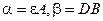
Второй способ.
Каждое 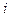 -ое уравнение делится на
-ое уравнение делится на 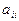
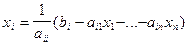
Тогда 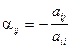 ,
, 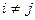 ,
, 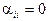 .
.
Тогда уравнение сходимости имеет вид
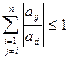 ,
, 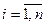
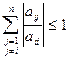 ,
, 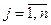
Эти неравенствабудут выполняться, если диагональные элементы будут удовлетворять условиям:
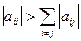 ,
, 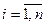 ,
,
то есть если модули диагональных коэффициентов для которого уравнения системы больше суммы модулей всех остальных коэффициентов.
Дата добавления: 2016-09-20; просмотров: 678;
