Общие выводы по задаче интерполяции
1. Для равноотстоящих узлов интерполирования лучше всего выбирать интерполяционные формулы Ньютона, при этом:
а) если значение в начале таблицы - 1ИФН
б) если значение в конце таблицы - 2ИФН
2. Существуют интерполяционные центральные формулы, позволяющие интерполировать в середине таблицы, используя близлежащие разности (Гаус, Стерлинг, Бессель)
3. Для неравноотстоящих узлов интерполирования существуют формулы Лагранжа, Ньютона.
4. Если количество узлов больше и существует возможность определения хотя бы первых производных в узлах, то лучше всего исрользовать интерполяцию сплайками.
5. Если существует возможность выбора узлов, то выбирают по условиям Чебышева, которое позволяет уменьшить погрешность аппроксимации.
6. Используя интерполяционные формулы, можно решать задачу обратного интерполирования.
7. Задача обратного интерполирования может быть использована при решении корней уравнения, а именно:
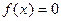 , необходимо найти корни. Составляем таблицу
, необходимо найти корни. Составляем таблицу 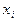
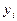 по формуле, а затем задаваясь значением
по формуле, а затем задаваясь значением  => ищат
=> ищат 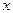 .
.
Дата добавления: 2016-09-20; просмотров: 634;
