Метод Гаусса. Схема с выбором главного элемента
1. Выбираем элемент 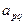 - наибольший по модулю и неявляющийся свободным членом.
- наибольший по модулю и неявляющийся свободным членом.
2. Вычисляем коэффициенты
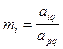 , для всех
, для всех 
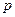 -тая строка называется главной строкой.
-тая строка называется главной строкой.
3. Из каждой неглавной строки вычитаем главную строку, умноженную на 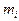 . В результате получим матрицу, у которой в
. В результате получим матрицу, у которой в  -ом столбце все коэффициенты нулевые.
-ом столбце все коэффициенты нулевые.
4. Преобразуем матрицу следующим образом: отбрасываем 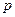 - (главную) строку и
- (главную) строку и  -й столбец. Получим матрицу
-й столбец. Получим матрицу 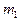 .
.
5. Делаем подобные преобразования над матрицей 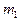 до тех пор, пока не получим одну строку из двух столбцов, которая является главной.
до тех пор, пока не получим одну строку из двух столбцов, которая является главной.
6. Для определения  . Объединим все главные строки, начиная с последней. После надлежащего изменения неизвестных получается система с треугольной матрицой.
. Объединим все главные строки, начиная с последней. После надлежащего изменения неизвестных получается система с треугольной матрицой.
При работе на ЭВМ при 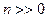 вывод главного элемента может оказаться достаточно трудоёмкой задачей. Поэтому практически в качестве главной строки берут первую строку, а в качестве главного элемента - наибольший по модулю элемент этой строки.
вывод главного элемента может оказаться достаточно трудоёмкой задачей. Поэтому практически в качестве главной строки берут первую строку, а в качестве главного элемента - наибольший по модулю элемент этой строки.
Пример: 
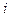
| 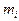
| 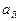
| 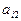
| 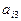
| 
| 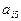
| 
| |
| -0,6 | -1 | |||||||
| I | 5 | -4 | -12 | -17 | ||||
| -0,4 | -1 | |||||||
| -0,2 | -5 | -3 | -1 | |||||
| -0,333 | 1,6 | 0,8 | -0,4 | -1,2 | 0,8 | |||
| II | -0,083 | 0,4 | 2,2 | -2,6 | -3,8 | -3,8 | ||
| -4,8 | 3,6 | -3,8 | 0,6 | -4,4 | ||||
| III | 0,571 | 2,0 | -1,665 | -1,0 | -0,665 | |||
| 2,5 | -2,915 | -3,75 | -4,165 | |||||
| IV | 0,572 | 1,141 | 1,713 | |||||
| V | 2,0 | |||||||
| VI | 3,0 | |||||||
| VII | -1,0 | |||||||
| VIII | 1,0 |

Достоинства метода
1. Если матрица вырождения, то перед исключением неизвестной главный элемент считается равным нулю => 
2. С помощью метода Гаусса можно вычислить определитель 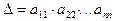 треугольной матрицы.
треугольной матрицы.
При большом числе неизвестных схема метода Гаусса, дающая точное решение, становится весьма сложной.
В этих случаях для нахождения корней системы лучше пользоваться приближёнными численными методами.
Метод итераций
Дана система уравнений
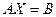
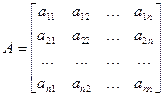
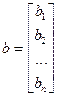
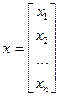
Можно привести систему к такому виду, чтобы диагональные элементы были отличные от нуля, то есть 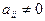 , тогда разрешая
, тогда разрешая 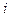 -тое уравнение относительно
-тое уравнение относительно  , получаем
, получаем
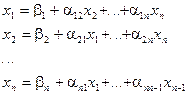 , (2)
, (2)
где  ,
, 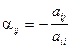 ,
, 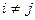 или
или  при
при 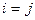
 ,
,  .
.
Тогда систему уравнений 2 можно записать в виде:
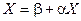 - итерационная формула.
- итерационная формула.
Таким образом, выбрав начальные значения 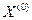

и так далее.
Итерации останавливаются, когда 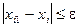 ,
, 
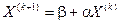
Дата добавления: 2016-09-20; просмотров: 1470;
