Численное решение систем нелинейных уравнений

Постановка задачи

Дана система линейных уравнений

(1)

Введём обозначения: вектор 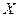- вектор аргументов:

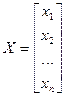
Аналогично вектор функций

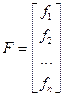
Тогда систему 1 можно переписать в виде:

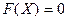
Система линейных уравнений в общем виде неразрешима. Поэтому мы будем рассматривать только численные методы решения системы линейных уравнений.

Метод Ньютона

Для уравнения имеет вид:

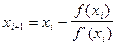
По анологии метод Ньютона для системы линейных уравнений

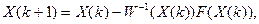
где 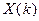- вектор аргументов на 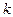-ом шаге итерации

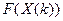- значения вектора функций (системы уравнений ) при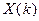

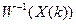- обратная матрица Якоби

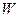- матрица, Якоби-матрица, состоящая из частных производных

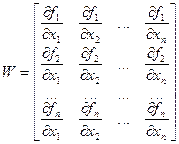
Вполне естественно очевидно, что формулу Ньютона можно применять в том случае, когда Якоби-матрица неособенная, невырождённая, то есть .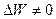

Пример:

Дано: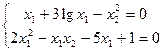

Матрица Якоби

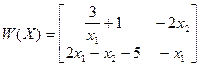
Превоначальная оцнка

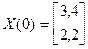
1)

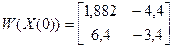
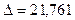
2)

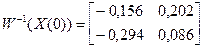
3)

- = - =

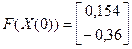
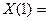
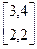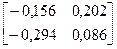
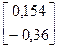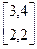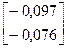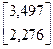
и так далее

Результаты итераций лучше всего сводить в таблицу

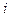
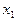
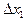
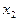
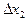
	3,4	0,097	2,2	0,076
	3,497		2,276

Прекращаем вычисления, когда 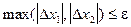- заданная точность.

Как и в любых численных методах встают следующие задачи: о сходимости метода и о выборе начального значения.