Достоинства метода итераций

1. Если итерации сходятся быстро, то есть для сходимости требуется менее 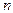итераций, то выигрыш во времени по сравнению с методом Гаусса:

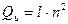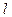, - число итераций

2. Погрешности округления в методе итераций сказывается значительно меньше, чем в методе Гаусса. Кроме того, метод итерации является самоисправляющимся, то есть отдельная ошибка запрещается в вычислениях, не отражаясь на конечном результате, то есть ошибочное приближение можно рассматривать как новый начальный вектор.

3. Метод итераций становится особенно выгодным при решении систем, у которых значительное число коэффициентов равно нулю.

4. Метод итераций легко программируется.

Метод Зейделя

Является модификацией метода итераций. Основная идея заключается в том, что при вычислении 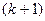-го приближения 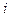-го корня используются уже вычисленные 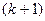приближённые корни .

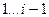Дано: ,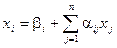

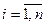
Выбираем начальное приближение:

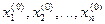
На 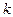-том шаге, согласно Зейделю строим приближение по следующим формулам:

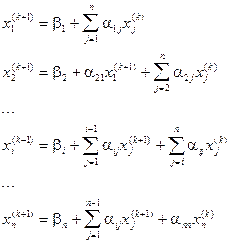
1. Метод Зейделя даёт полную сходимость по сравнению с методом итерации, но приводящий к громоздким вычислениям.

2. Теорема: Для существования единственного решения системы сходимости метода Зейделя достаточно выполнение хотя бы одного из двух условий:

1) ,

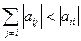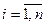
2) матрица 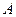- симметричная положительно определённая (все её соответственно значения положительны)