Метод Гаусса. Схема единственного деления

Наиболее распространённым приёмом решения системы линейных уравнений является метод Гаусса или метод последовательного исключения неизвестных.

Рассмотрим для простоты систему линейных алгебраических уравнений 4-го порядка:

1. Выбираем ведущий элемент

2. Поделив первое уравнение на 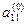, получаем

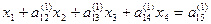, (2)

где , ,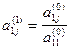

3. Исключаем переменную 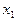из всех последующих уравнений, начиная со второго, путём вычитания уравнения 2, умноженного на коэффициент, стоящий при 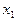в соответствующем уравнении. Получаем

,

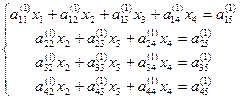где , ,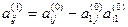

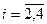4. Выбираем ведущий элемент во втором уравнении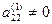

и так далее.

Если 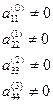, то получим систему

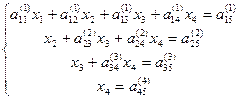, (3)

то есть матрица 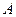имеет диагональный вид:

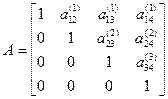
Из системы 3 отыскиваем 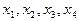следующим образом

, (4)

Процесс приведения матрицы к треугольному виду 3 называется прямым ходом, а нахождение корней по 4 обратным ходом.

Пример: прежний, но методом Гаусса. Приводит к системе уравнений:

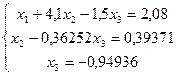- прямой ход

- обратный ход

Существует схема единственного деления, которая используется при дирном счёте, но мы либо рассмотрим её на практике, либо вообще не будем рассматривать.

То есть в нашем курсе мы ориентируемся на вычислительную технику и все методы интересуют как алгоритмы.