Первые железные дороги. 4 страница

При движении по подъему суммарное сопротивление всегда направлено в сторону, противоположную направлению движения, т.е. положительно. Поскольку дополнительное сопротивление от уклона W, по абсолютной величине может превышать сумму основного сопротивления и дополни­тельного сопротивления от кривой W_Q+W_rt то при движении по достаточ­но крутому спуску суммарное сопротивление может быть направлено в сторону движения поезда, т.е. отрицательно.

Тормозная сила поезда. Торможение может осуществляться двумя спосо­бами: 1 — прижатием тормозных колодок к ободам колес подвижного со­става или к тормозным дискам, укрепляемым на колесных парах (механи­ческое торможение)\ 2 — использованием тормозной силы, создаваемой электродвигателями локомотивов (электродинамическое торможение).

В обоих случаях тормозная сила реализуется вследствие сцепления ко­леса и рельса. Как и сила тяги, она приложена в точке касания колеса и рельса, но направлена в сторону противоположную движению. Чтобы не допустить юза (заклинивания колес), который приводит к интенсивному износу колес и рельсов, при торможении необходимо обеспечить достаточ­но высокий коэффициент сцепления колеса с рельсом. Это требует, как уже отмечалось, чистой поверхности рельсов, отсутствия на них следов смазки, грязи.

При механическом торможении тормозная сила поезда 5_Т, Н, определя­ется в зависимости от общей силы нажатия тормозных колодок на оси по­езда

В_т = ЮЧрЫр, (2.19)

где ZK_P - сумма расчетных сил нажатия на тормозные оси поезда, кН; в приложе­нии 1 приведены указанные в ПТР и Справочнике по тяговым расчетам [11] значе­ния Лр для вагонов и локомотивов при автоматическом торможении; <р_кр — расчет­ный коэффициент трения тормозной колодки о колесо.

Расчетный коэффициент трения вычисляется по следующим формулам: при чугунных колодках

0,27(v + 100) О»' 5 v + 100 ⁽¹²⁰⁾

при композиционных колодках

0,36(v + 150) ^ф»⁼ 2 v + 150 ⁽²'²°'^а)

где v — скорость поезда, км/ч.

Удельная тормозная сила поезда, Н/кН,

1К_В

где Э_р = ^р ₊ q^ ~ расчетный тормозной коэффициент поезда, кН/кН.

Определим удельную тормозную силу поезда, состав которого состоит из 20 груженых и 40 порожних четырехосных вагонов. Масса тары (собственная масса) вагона — 23,5 т, масса брутто груженого вагона — 83 т. Вычислим тормозную силу при скоростях 50 и 100 км/ч на спусках до 20 %о. Тормозные колодки чугунные.

Тормоза грузовых вагонов при чугунных колодках включают на груженый ре­жим при полезной загрузке (массе груза в вагоне), приходящейся на одну ось, бо­лее 6 т; на средний режим — при загрузке до 6 т; на порожний — при загрузке до 3 т.

Поскольку масса груза в груженом вагоне составляет 83 - 23,5 = 59,5 т, т. е. бо­лее 6 т на ось, то при груженом режиме расчетная сила нажатия тормозных коло­док на ось составит 68,7 кН (см. приложение 1). Расчетная сила нажатия колодок на ось порожнего вагона составляет 34,3 кН (там же).

Суммарное расчетное нажатие тормозных колодок на оси вагонного состава

ZK_P= 68,7 ■ 4 ■ 20 + 34,3 ■ 4 ■ 40 = 10988 кН[5].

Расчетный коэффициент трения тормозных колодок по формуле (2.20): при скорости 50 км/ч

0,27(50 + 100)

Ф.„ =------------------ = 0,116;

^р 5-50 + 100

при скорости 100 км/ч

О^ООн-ШО) ^кр 5 100 + 100

Расчетный тормозной коэффициент вагонного состава

Не.. = 0,43.

Qg 2600 9,81

Удельная тормозная сила по формуле (2 21): при скорости 50 км /ч

b_T= 10³ 0,1 16 0,43 = 49,88 Н/кН ,

при скорости 100 км/ч

6_Т= 10³ 0,090 0,43 = 38,70 Н/кН

При композиционных тормозных колодках и скоростях более 50 км/ч эффективность действия тормозов выше по сравнению с чугунными ко­лодками. Так, при скорости 90 км/ч композиционные колодки эффектив­нее на 10%, при скорости 100 км/ч - на 20% [11].

Электродинамическое торможение локомотивов основано на использо­вании свойства обратимости электрических машин. При включении тяго­вых электродвигателей локомотива на генераторный режим на валу образу­ется вращающий момент, направленный в сторону, противоположную движению. Вырабатываемая при этом электровозами электрическая энер­гия может возвращаться в контактную сеть (рекуперативное торможение) или погашаться в резисторах (при электрической и тепловозной тяге) — резисторное торможение, что менее эффективно. В ПТР приведены тор­мозные характеристики электровозов при рекуперативном и реостатном (резисторном) торможениях, определяющие тормозную силу которую может реализовать электровоз при соответствующей скорости.

2.2 Взаимодействие сил, приложенных к поезду

Характер и режимы движения поезда. Характер движения поезда зависит от соотношения сил, действующих на него. Если равнодействующая сила направлена в сторону движения, она считается положительной — поезд движется ускоренно; если равнодействующая направлена против движе­ния, она отрицательна — поезд движется замедленно. Если равнодейст­вующая равна нулю, то движение поезда равномерное

Различают следующие режимы движения поезда:

режим тяги — двигатели локомотива включены; равнодействующая си­ла равна разности сил тяги и суммарного сопротивления движению: R = F_K- Ж_к;

режим холостого хода — двигатели выключены; равнодействующая равна суммарному сопротивлению при холостом ходе R = W_KX;

режим торможения — двигатели выключены и включены тормоза, рав­нодействующая сила равна сумме сопротивления движению при холостом ходе и тормозной силы R = W_KX+ В,.

6) б) (Ь-Щ),Н/кН 8 6 4 2 0 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 Ч648-^ох,Н/кН "Г- 1 -Ыох*Ът),НМН Рис. 2.7. Диаграммы удельных равнодействующих сил в режимах: а — тяги, б — холостого хода, в — служебного торможения, г — экстренного торможения

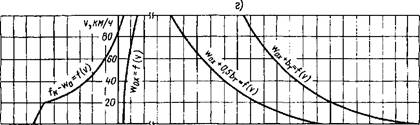
Диаграммы удельных равнодействующих сил. Анализировать характер движения поезда в различных режимах удобно по диаграммам удельных равнодействующих сил, т.е. по графикам зависимости этих сил от скоро­сти. В качестве примера показаны диаграммы удельных равнодействующих сил для состава массой 4500 т при тепловозе 2ТЭ10М (рис. 2.7). Диа­граммы строят для условий движения поезда на площадке, т.е. учитывают только основное средневзвешенное сопротивление движению поезда w₀ и w_0x.

При построении диаграмм используется следующее правило: влево от оси ординат откладывают положительные равнодействующие силы, впра­во — отрицательные. Равнодействующая сила в режиме тяги г = f_K — w₍₎ (см. рис. 2.7,а) с увеличением скорости уменьшается, поскольку уменьша­ется сила тяги и возрастает сопротивление движению. В данном примере при v = 85 км/ч равнодействующая сила равна нулю: при этой скорости сила тяги и основное сопротивление движению поезда равны. При более высоких скоростях w₀ > f_K и равнодействующая становится отрицатель­ной — направлена против движения поезда.

Равнодействующая сила при движении на площадке в режиме холостого хода отрицательна - r= — w_0x (см. рис. 2.7,6); абсолютное значение ее уве­личивается с ростом скорости.

Равнодействующую силу при торможении определяют в двух вариантах: служебное торможение (см. рис. 2.7,в), когда в грузовых поездах использу­ют 50% расчетной тормозной силы г = - (w_0x + 0,5b_T), а в пассажирских поездах — 60% (при плановых остановках или при торможении для преду­смотренного графиком движения ограничения скорости); экстренное торможение г = — (щ_)х + Ь_л ) (см. рис. 2.7,г), когда полностью используют тормозную силу (для остановки поезда в непредвиденных случаях). При торможении равнодействующая сила отрицательна. С увеличением скоро­сти ее абсолютное значение уменьшается, так как с ростом скорости суще­ственно уменьшается тормозная сила (вследствие уменьшения коэффици­ента трения ф_кр — см. формулы (2.20) и (2.20,а).

По диаграмме удельных равнодействующих сил можно судить о харак­тере движения поезда в данный момент.

В примере на рис. 2.7,а при трогании поезда с места на площадке на него дей­ствует положительная удельная равнодействующая сила, равная 13 Н/кН, следова­тельно, поезд движется ускоренно. Если площадка длинная, то движение будет ус­коренным, пока скорость не достигнет 85 км/ч. В этот момент равнодействующая сила станет равной нулю и начнется равномерное движение. Если бы поезд после спуска вышел на площадку со скоростью 100 км/ч, то на него действовала бы от­рицательная равнодействующая сила —1 Н/кН. Под действием этой силы движение будет замедленным, скорость уменьшается, стремясь к 85 км/ч. Если площадка длинная, то по достижении этой скорости движение установится равномерным.

При движении поезда по площадке в режиме холостого хода под дейст­вием отрицательной равнодействующей силы скорость поезда всегда стре­мится к нулю. То же происходит и при торможении.

Чтобы перейти к условиям движения на любом уклоне, вспомним, что на уклоне возникает дополнительное удельное сопротивление w„ Н/кН, численно равное уклону /_к, %с. Суммарное удельное сопротивление при движении на подъеме больше основного сопротивления на величину w„ а при движении на спуске меньше основного сопротивления на ту же вели­чину. Поэтому, чтобы получить удельную равнодействующую силу на ук­лоне, нужно в случае подъема вычесть из удельной равнодействующей си­лы на площадке число, равное уклону и выраженное в Н/кН, а в случае спуска - прибавить то же число. Это равносильно переносу оси ординат диаграммы удельных равнодействующих сил в случае подъема — влево на величину i_K , Н/кН, а в случае спуска — вправо на ту же величину.

Так, если принять подъем 2%с (сместить ось ординат на 2 Н/кН влево от ос­новной оси на рис.2.7), то удельная равнодействующая сила при трогании поезда на этом подъеме равна +11 Н/кН и в случае длинного подъема скорость поезда возросла бы до 60 км/ч, после чего движение станет равномерным (удельная рав­нодействующая сила при этой скорости на подъеме 2%о равна нулю). Если бы по­езд вышел на подъем 2%о со скоростью 100 км/ч, то на него действовала бы отри­цательная равнодействующая сила, равная —3 Н/кН, и скорость поезда снижалась, стремясь к тому же значению 60 км/ч.

При движении в режиме тяги и холостого хода на любом уклоне скорость поезда стремится к определенному значению, которое называют установившейся скоростью. В отдельных случаях эта скорость может быть равна нулю, а также может быть больше конструкционной скорости локомотива. В других случаях установившаяся скорость соответствует точке пересечения диаграммы удельных равнодействующих сил с осью ординат, проведенной с учетом крутизны рассматриваемого уклона. Если поезд выходит на уклон с меньшей скоростью, то скорость растет, приближаясь к установившейся; если скорость при выходе на данный уклон больше установившейся, то она снижается, приближаясь к послед­ней.

В примере на рис. 2.7 в режиме тяги скорость 85 км/ч - установившаяся ско­рость v_ytT на площадке, а 60 км/ч — v_scl на подъеме 2%о. При движении в режиме холостого хода на спуске 2%с v_JCT = 70 км/ч. При том же режиме движения на спуске 4%е установившаяся скорость могла быть больше конструкционной скоро­сти. Поэтому, чтобы скорость поезда на этом спуске не превысила любое заданное значение в пределах 100 км/ч, необходимо применить регулировочное торможение. При движении в режиме тяги на спуске 2%о скорость поезда также могла превы­сить конструкционную. Поэтому, чтобы на данном спуске поддерживать скорость, например, 90 или 100 км/ч, следует использовать режим ограниченной тяги, когда сила тяги реализуется при ограниченной мощности локомотива

Если же в режиме холостого хода поезд движется по площадке, то установив­шаяся скорость равна нулю и поезд будет снижать скорость до остановки Анало­гично при движении в режиме тяги на подъеме 14%о v_ycT = 0 и скорость поезда также будет падать до нуля.

2.3. Определение скорости движения и времени хода поезда

Скорость и время хода поезда определяют численным интегрированием уравнения движения поезда

— = 120r( v), (2.22)

dt

где dv/dt — ускорение поезда, км/ч², r(v) — удельная равнодействующая сила, Н/кН

Заменяя производную в уравнении (2.22) разностным отношением, по­лучим

^ = 120r(v_cp), (2.23)

At

где v_Cp — среднее значение скорости в интервале Av, который для обеспечения не­обходимой точности расчетов принимается согласно ПТР не более 5— 10 км/ч

За время At, ч, поезд пройдет путь, км, AS = У_срД/. Умножая обе части уравнения (2.23) на v_cp, после преобразования получим

v Д v 120r(v_cp)

Поскольку v_cp = - и Av = v₂ — v_h то формула (2.24) получает сле­дующее выражение (AS — в метрах):

(v²-v²Vl0³ 4,17 (v,² - v,²)

= -------- ^L—=------------ —г——. (2.25)

2 120r(v_cp) r(v_cp)

Время хода поезда, мин, при изменении скорости от v, до v₂ можно оп­ределить по средней скорости на участке пути AS, м:

= (2.26)

Используя зависимость (2.25) можно рассчитать протяженность пути S определенного профиля, на котором скорость поезда изменяется от на-

разгона

чальной v_H до конечной v_K. Для этого суммируют значения Д5 в пределах от v_H до v_K:

5=1" A5(v).

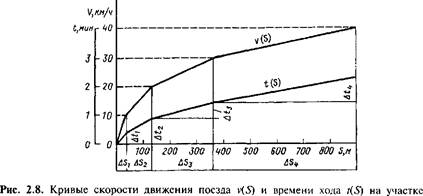
Ниже, применительно к примеру, рассмотренному в п. 2.2, приведен пример определения протяженности пути разгона поезда на площадке при трогании с мес­та и до скорости 40 км/ч, а также продолжительности этого разгона. Результаты расчета приведены в табл. 2.2, а зависимости v(5) и t(S) - на рис. 2.8.

На перегоне, где уклоны элементов профиля различны, непосредствен­ное использование формулы (2.25) неудобно, поскольку нельзя зара­нее установить значение конечной скорости в конце элемента, когда при переходе к другому элементу профиля изменяется равнодействующая сила, зависящая от уклона пути. При определении скорости движения поезда на перегоне целесообразно преобразовать формулу (2.25) следующим обра­зом:

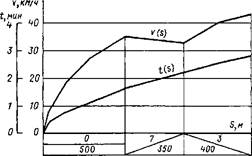Рис. 2.9. Кривые скорости движения и времени хода поезда на перегоне

Задаваясь начальной скоростью v, и отрезком пути AS в пределах данно­го элемента профиля, по приведенной формуле можно определить ско­рость v₂. Однако при этом равнодействующая сила не может быть установ­лена при средней скорости в пределах искомого интервала Av и приходится ее принимать в зависимости от начальной скорости в интервале Av, т. е. Kv,):

Г AS г (v.)

Н"^?+ V7 ■ ⁽²'²⁷⁾

Расчет по формуле (2.27) содержит некоторую погрешность, однако, учитывая указанное выше ограничение интервала Av, обеспечивает прием­лемую точность результата.

Рассмотрим пример определения скорости и времени хода поезда по участку пу­ти, продольный профиль которого (уклоны в %о и длины элементов в метрах) при­веден на рис. 2.9, а данные расчета скоростей по формуле (2.27) и времени хода по формуле (2.26) содержатся в табл. 2.3.

Как следует из рис. 2.8 и 2.9, полученные расчетами данные позволяют определить скорость движения и время хода поезда в любой точке пути.

Рассмотренные методы численного интегрирования уравнения движе­ния поезда позволяют автоматизировать расчеты скорости движения и времени хода поезда.

Для некоторых расчетов при проектировании железных дорог (напри­мер, для предварительного размещения осей станций и разъездов) время хода поезда определяют приближенным методом установившихся скоро­стей.

В результате расчета удельных равнодействующих сил определяют уста­новившиеся скорости движения поезда на разных уклонах (см. п. 2.2). Ис­ходя из предположения, что на каждом элементе профиля поезд быстро достигает установившейся скорости v„ км/ч, вычисляют время хода поезда на 1 км пути при данном уклоне t, = 60/v„ мин/км, а затем время хода по­езда по участку определяют по формуле

т= Щ,

где /, — длина отдельных элементов профиля, км.

Если расчет выполняют в пределах перегона между пунктами останов­ки, то к времени хода, вычисленному по приведенной формуле, добавляют поправку на разгон и замедление поезда /_pj, в среднем принимая ее равной 3 мин.

2.4. Решение тормозных задач

Как следует из п. 2.3, используя формулу (2.25), можно определить про­тяженность пути, проходимого поездом при торможении от заданной на­чальной скорости v_H до остановки. При фиксированной v_H протяженность этого пути зависит от удельной равнодействующей силы г = w_K, + b, (экс­тренное торможение) или г = w_KX + ab_T (служебное торможение: а равно 0,5 или 0,6 — см. п. 2.2). Сила г, в свою очередь, определяется значением при­веденного уклона пути /, по которому движется поезд, поскольку и>_кх = w_0x ± / _к, и величиной расчетного тормозного коэффициента д_Р, от ко­торого зависит удельная тормозная сила /;,, вычисляемая по формуле (2.21).

В практике тяговых расчетов наряду с задачей определения протяжен­ности пути торможения при заданных v„ /_к и i3_p возникает необходимость определить допускаемую скорость движения поезда на данном уклоне при соответствующем значении и установленной длине тормозного пути.

Тормозным путем S_T называется расстояние, проходимое поездом от момента перевода ручки крана машиниста или стоп-крана в тормозное по­ложение и до полной остановки поезда. Этот путь вычисляют как сумму пути подготовки к торможению S_n и действительного пути торможения S_A, рассчитываемого по формуле (2.25). Путь S„ пассажирские поезда проходят за несколько секунд, а грузовые — за время продолжительностью до полу- тора-двух десятков секунд (в зависимости от длины поезда и крутизны спуска), в течение которого постепенно нарастает давление воздуха в тор­мозных цилиндрах.

Допускаемую длину тормозного пути при экстренном торможении грузовых поездов и пассажирских, следующих со скоростью не более 100 км/ч, принимают 1000 м, если наибольшая крутизна спус­ков на перегоне менее 6%с, и 1200 м на более крутых спусках. Для пассажирских поездов, обращающихся со скоростями до 120 км/ч, протяженность S_T принята (в зависимости от указанной выше крутиз­ны спусков) соответственно 1200 и 1300 м, а при скоростях 160 км/ч и бо­лее - 1600 и 1700 м [11].

Для облегчения тормозных расчетов в ПТР содержатся номограммы тормозных путей грузовых и пассажирских поездов при экстренном торможении на площад­ке и спусках различной крутизны (эти номограммы для грузовых поездов приве­дены в приложении 2).

Пример пользования номограммами пока­зан на рис. 2.10. Если грузовой поезд, у кото­рого расчетный тормозной коэффициент 0_Р = 0,33, движется по спуску 8%о со скоро­стью 70 км/ч, то при экстренном торможении £_т= 5„ + составит 800 м. При наибольшем допускаемом значении тормозного пути 1200 м и указанной величине максимальная скорость поезда на спуске 8%с определена в размере 85 км/ч.

Тормозные пути на номограммах рас­считаны для составов длиной до 200 осей. Для более длинных составов (до 300 осей)

тормозные коэффициенты, указанные на номограммах, следует уменьшить на 10%, а для поездов до 400 осей — на 15% [11].

2.5. Расчеты массы состава и длины поезда

Расчет массы состава при установившемся движении. При проектирова­нии новых железных дорог массу состава, как правило, определяют из ус­ловия равномерного движения поезда с расчетной скоростью v_p на руково­дящем подъеме, т.е. наиболее крутом подъеме неограниченного протяже­ния (см. гл. 3). При этом сила тяги локомотива равна суммарному сопро­тивлению движению поезда, Н,

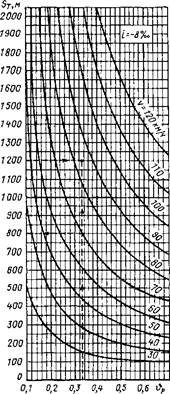Рис. 2.10. Кривые тормозного пути грузового поезда при экс­тренном торможении на спуске / = -8 %о

= К = К + ^w.)^pS + К + ^w.)Qs = (Ч + 'р)Pg + К + i„)Qg ,

откуда масса состава, т

_Q=^f«p>-K⁺'p)ft, (2.28)

где /^Г_К(pi ^- расчетная сила тяги локомотива, Н, при скорости v_p, /_р - руководящий уклон, %о (равен дополнительному удельному сопротивлению от уклона, Н/кН), w'₀ и w"_a — основные удельные сопротивления движению локомотива и состава вагонов, Н/кН, при скорости v_p

Если перейти от основного удельного сопротивления движению локо­мотива и вагонов к средневзвешенному сопротивлению поезда w₀ согласно формуле (2.8), то масса состава

Q = , ^/"^к"'\ -Р. (2.29)

К + i_p)g

Однако для определения величины щ нужно знать массу состава, т. е. искомую величину. Поэтому формулу (2.29) можно использовать только принимая w₀ а и>„ . Расчет по этой формуле дает несколько завы­шенный результат по сравнению с формулой (2.28), и, хотя погрешность составляет менее 1%, при больших значениях массы состава эта по­грешность может быть сопоставима с требуемой точностью расчетов (со­гласно ПТР масса составов грузовых поездов принимается с округлением до 50 т).

Значения расчетной скорости v_p и расчетной силы тяги грузовых локо­мотивов F_K(р) в соответствии с нормами ПТР приведены в приложении 3.

В Правилах тяговых расчетов указано также, что для определения массы состава при проектировании новых железных дорог и электрификации действующих линий силу тяги электровозов следует принимать на 5%, а тепловозов на 7% меньше расчетной, предусмотренной Правилами. С уче­том этого указания в приложении 4 приведены значения массы составов грузовых поездов при различных руководящих уклонах, рассчитанные по/ формуле (2.28) применительно к четырехосным вагонам на роликовый подшипниках при массе, приходящейся на ось q₀ = 17,5 т, и для условий движения по бесстыковому пути.

Определим массу состава, которую тепловоз 2ТЭ116 может провести по бессты­ковому пути на руководящем уклоне /_р = 15%о.

Значение расчетной силы тяги F_K(P), Н, расчетную скорость v_p, км/ч, и расчетную массу локомотива Р, т, примем по таблице приложения 3

Основное удельное сопротивление движению локомотива определим по форму­ле (2.3)

< = 1,9 + 0,008 24,2 + 0,00025 24,2² = 2,24 Н/кН.

Средневзвешенное основное удельное сопротивление движению состава вагонов определим по зависимости, полученной в примере п 2 1

w; = 0,90 + 0,0179 24,2 + 0,000119 24,2² = 1,40 Н/кН -50-

Ст. А 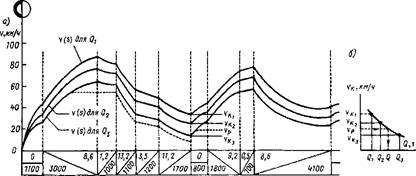Рис. 2.11. К определению массы состава при неустановившемся движении: а — зависимости v(5); б — зависимость v„(Q)

Расчетная масса состава, т, по формуле (2.28)

496400( 1 - 0,07) - (2,24 + 15)276 -9,81 _ _2т (1,40 + 15)9,81

Расчетная масса состава, т, по формуле (2.29) при w,

496400(,- 0,07) _ ₂₇₆ ^₅₉₃ (1,40 + 15)9,81

Разница в результатах расчетов по формулам (2.28) и (2.29) составляет 14 т (0,5%). С учетом округления массы состава до 50 т следует принять Q = 2600 т.

Расчет массы состава при неустановившемся движении. На существующих железных дорогах, особенно строившихся давно, наряду с затяжными подъемами встречаются короткие, но более крутые подъемы, которые мо­гут оказаться труднейшими для преодоления их поездом. По таким подъе­мам движение может быть неустановившимся, и тогда расчетную массу состава целесообразно определять методом подбора.

По крутизне подъема, меньшей, чем самый крутой подъем на участке, рассчитывают массу состава £>, по формуле (2.28) или (2.29) (принимая н>₀ = ), и для состава данной массы определяют скорость движения поез­да на перегоне. Если скорость поезда в конце труднейшего подъема v_K] (на рис. 2.11,а — это подъем с уклоном 11,2%с) больше расчетной, то массу состава увеличивают на несколько сотен тонн до значения Q₂ и вновь оп­ределяют скорость поезда. При v_k2 > v_p принимают еще большее значение массы состава (результаты указанных расчетов иллюстрирует рис. 2.11,а). Если в результате очередной попытки скорость в конце труднейшего подъ­ема оказывается меньше расчетной скорости, то следует соответственно уменьшить массу состава. Так поступают до тех пор, пока конечная ско­рость будет равна расчетной. Чтобы ограничиться, как правило, тремя по­пытками, можно построить по трем значениям v_K график зависимости v_K(Q) (см. рис. 2.11,6), и, отложив на оси ординат значение расчетной ско­
рости для данного типа локомотива, по оси абсцисс определить расчетную массу состава.

Масса состава при неустановившемся движении поездов в большой сте­пени зависит от условий накопления кинетической энергии поезда на уча­стках, предшествующих расчетному подъему. Так, если скорость поезда в конце спуска 8,6%о или на подъеме 1,2%с ограничена значением 60 км/ч (см. штриховую линию на рис. 2.11,о), то расчетная масса состава окажется меньше, чем в случае, когда нет ограничения скорости. Следовательно, для обеспечения больших значений массы грузовых поездов путейцам необхо­димо создать на участках, предшествующих расчетным подъемам, возмож­ность реализации максимальных скоростей движения поездов. Ограниче­ния скоростей на этих участках особенно нежелательны.