ОСНОВЫ ТЕОРИИ РАБОЧИХ ПРОЦЕССОВ В ЦИЛИНДРЕ ДИЗЕЛЯ § 1.1. Идеальный цикл дизеля 13 страница
Теплоемкость смеси подсчитывается с учетом относительной доли воздуха и чистых продуктов сгорания cv = с\ rr + c”v г”.
При такой постановке в задачах численного моделирования рабочих процессов влияние сорта топлива учитывается только величиной QH , задаваемой в исходных данных. Устранить отмеченные недостатки можно, если ввести в алгоритм расчета определение теплоемкости и газовой постоянной с учетом элементарного состава топлива и влагосодержания воздуха.
Положим, что 1 кг топлива включает Н кг водорода, С кг углерода, О кг кислорода и S кг серы. Тогда продукты полного сгорания топлива будут содержать:
(11/3) С кг углекислого газа СО2;
9 Н кг водяного пара Н2О;
2 S кг двуокиси серы SO2;
0,77G0 кг азота N2.
Масса чистых продуктов сгорания при сжигании 1 кг топлива составит (Go+1) кг.
Массовые доли отдельных компонентов в составе продуктов сгорания определяются по следующим соотношениям:
_ 3>67 - 9 г/. „ _ 2 с.
ГС02 — г 1 С’ ГН20 ~ п , I ’ rS02 ~ ,1 1 Сг0 + 1 Cjq + 1 Сг0 + 1
г =^-G G0 +1 °‘
Очевидно, что rcol + rH10 + rSQ2 +rN2= 1.
Теоретическая масса воздуха, необходимого для сжигания 1 кг топлива:
1 (SC + 24H Л
 + S-0
+ S-0
 V 3 у
V 3 у
Значения термодинамических величин для всех компонентов смеси газов в цилиндре дизеля приведены в табл. 6.1. Здесь же указан диапазон температур, для которого справедлива аппроксимирующая формула.
| Вещест во | Коэффициенты в формуле теплоемкости | Г азовая постоянная кДж/(кг-К) | Темпера турный интервал, | ||
| а | Ъ | С | |||
| о2 | 0,7249 | 1,06-1 O'4 | -1,178-104 | 0,260 | 298-3000 |
| сог | 0,8155 | 2,057-104 | -1,942-104 | 0,1891 | 298-2500 |
| нго | 1,205 | 5,952-Ю-4 | 1,86-103 | 0,4617 | 298-2500 |
| so2 | 0,536 | 1,964-1 O'4 | -8,841-Ю3 | 0,130 | 298-1800 |
| *2 | 0,70 | 1,5255-1 O'4 | 0,2975 | 298-2500 |
| Таблица 6.1 |
 Пользуясь данными табл. 6.1, можно вычислить коэффициенты аппроксимирующих формул для сухого воздуха, чистых продуктов сгорания с учетом элементарного состава топлива и водяного пара. Рассматривая сухой воздух как смесь (масса 1 кг), состоящую из 0,77 кг азота и 0,23 кг кислорода, получим:
Пользуясь данными табл. 6.1, можно вычислить коэффициенты аппроксимирующих формул для сухого воздуха, чистых продуктов сгорания с учетом элементарного состава топлива и водяного пара. Рассматривая сухой воздух как смесь (масса 1 кг), состоящую из 0,77 кг азота и 0,23 кг кислорода, получим:
а' = aN2 0,77 + а02 0,23 = 0,7 • 0,77 4- 0,7249 • 0,23 = 0,705.
Таким же образом подсчитываются коэффициенты V ,cf и газовая постоянная воздуха. Окончательно запишем:
с' =0,705+ 1,4185-10’4Г------ R’ = 0,28722. (6.21)
v j12
Для чистых продуктов сгорания с учетом термодинамических параметров компонентов из таблицы 6.1 и их долевого содержания в смеси получим:
48R7
с" = 0,76+ 1,959-10"4Гр-; R" = 0,2887. (6.22)
v 2
Для водяного пара:
с" = 1,205+ 5,952-10~474^s Л” = 0,4617. (6.23)
v 2
Удельная изохорная теплоемкость и газовая постоянная для трехкомпонентной смеси газов после расчета указанных физических величин для воздуха, чистых продуктов сгорания и водяного пара определяются по формулам:
cv =c/4cvVff + cvV; R = R'r’ + R”r” + Rmrm.
§ 6.6. Рабочие процессы в газовоздушном тракте и турбокомпрессоре
Для того чтобы получить замкнутую модель, необходимо дополнить систему дифференциальных уравнений (6.10), (6.13), (6.17) и (6.20) уравнениями рабочих процессов в выпускном коллекторе, газовой турбине, центробежном компрессоре, воздухоохладителе и продувочном ресивере. При этом необходимо учитывать, что в многоцилиндровом дизеле параметры в указанных элементах системы воздухоснабжения являются итогом работы всех цилиндров. Известны два подхода к решению задачи численного моделирования процессов в многоцилиндровых ДВС.
В первом из них моделируется полноразмерный двигатель, т. е. параллельно ведется расчет процессов во всех цилиндрах. Этот подход обладает тем преимуществом, что можно моделировать работу дизеля с различными g4 по цилиндрам, учитывать другие «индивидуальные» условия работы в каждом из них, т.е. математическая модель, составленная таким образом, наиболее полно описывает реальный двигатель. Для реализации такой модели требуется ЭВМ с большим объемом оперативной памяти и высоким быстродействием.
В большинстве используемых в настоящее время математических моделей расчет рабочего процесса осуществляется только в одном цилиндре. В то же время при расчете процесса выпуска газов из цилиндра учитывается влияние процессов выпуска из других цилиндров, объединенных в выпускной коллектор. Для этого формируются массивы значений расходов и энтальпий тазов, выходящих из цилиндра, в зависимости от угла поворота кривошипа и считается, что процессы выпуска газов из остальных цилиндров сдвинуты по фазе, которая в градусах угла поворота кривошипа равна: A<p = 360m/i, где т - коэффициент тактности двигателя; i - число цилиндров, объединенных в один коллектор. При этом принимается допущение о полной идентичности всех цилиндров и протекающих в них процессов. Этот метод использован в реализованном нами алгоритме для численного моделирования рабочих процессов судовых дизелей на персональных ЭВМ.
При описании рабочего процесса в выпускном коллекторе, так же как и для рабочего цилиндра, используются уравнения: первого закона термодинамики, массового баланса и состояния. Эти уравнения записываются следующим образом:
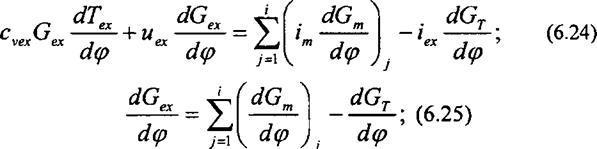 j
(6.26)
j
(6.26)
|
где Gex, Тех s Рех ~ масса, температура и давление газов в выпускном коллекторе; cvex> ц^ - удельные: изохорная теплоемкость, энтальпия и внутренняя энергия газов в выпускном коллекторе; Gm и im - масса и удельная энтальпия поступающих из цилиндра в коллектор газов; Vex- объем выпускного коллектора; GT - масса газов, поступающих в турбину.
Решение системы уравнений (6.24) - (6.26) осуществляется численным методом. Из уравнения (6.24) на каждом шаге счета определяется dTex!d(p, затем численным интегрированием этой функции - Тех. Давление в выпускном коллекторе определяется из уравнения состояния (6.26). Расчет термодинамических величин (cv, и, R, i) ведется с учетом реального состава смеси газов в выпускном коллекторе, т. е. по тем же уравнениям, что и для цилиндра. Тем самым учитывается влияние состава и вида топлива, влагосодержания атмосферного воздуха на работу газовой турбины.
 В общем случае давление в выпускном коллекторе отличается от давления за выпускными органами рг. Это связано с тем, что в приведенном выше алгоритме учитывается изменение р вызванное преобразованием кинетической энергии газов, поступающих из цилиндра в выпускной коллектор. При расчете процесса выпуска по уравнению (6.20) давление за выпускными органами следует принимать равным:
В общем случае давление в выпускном коллекторе отличается от давления за выпускными органами рг. Это связано с тем, что в приведенном выше алгоритме учитывается изменение р вызванное преобразованием кинетической энергии газов, поступающих из цилиндра в выпускной коллектор. При расчете процесса выпуска по уравнению (6.20) давление за выпускными органами следует принимать равным:
(6-27)
где £вк - коэффициент гидравлических потерь в выпускном
коллекторе; Сех = GT vex /fBK - скорость газов в выпускном коллекторе; - удельный объем газов в выпускном коллекторе; fBK - площадь сечения выпускного коллектора; g - ускорение свободного падения.
Необходимо отметить, что для дизелей с изобарным наддувом, имеющих единый для всех цилиндров выпускной коллектор большого объема, можно принять гипотезу о том, что параметры газа во всех его точках одинаковы, и применять рассмотренный выше алгоритм расчета.
Судовые среднеоборотные четырехтактные дизели, как правило, имеют импульсную систему наддува с разделенным на несколько групп выпускным коллектором. При этом длины и объемы патрубков для разных групп цилиндров могут существенно отличаться. Из отмеченного следует, что величины Тех, рех и рг в каждой группе будут различными (существенное отличие температур отработавших газов по отдельным цилиндрам в дизелях с импульсным наддувом хорошо известно из опыта эксплуатации). Таким образом, применение "одноцилиндровой" модели следует ограничить чисто учебными целями, когда не требуется точное соответствие расчетных показателей рабочих процессов данным эксперимента, а важен лишь качественный итог расчетного исследования. В данном случае в исходных параметрах задаются усредненные значения объемов и сечений выпускных патрубков.
Расчет рабочего процесса в газовой турбине ведется по упрощенной методике, суть которой состоит в следующем. Турбина рассматривается как эквивалентное сопло, имеющее эффективное проходное сечение fjfT. Расход газа через турбину определяется по формуле (6.20). Давление на входе в сопловой аппарат турбины р\ принимается равным рех, за сопловым аппаратом:
где рот - давление газов за турбиной; р - степень реактивности турбины; к - срех/ cvex - показатель адиабаты.
Алгоритм и программа численного моделирования рабочих процессов дизеля построены таким образом, что в течение расчета одного цикла параметры воздуха в продувочном ресивере считаются постоянными. Это позволяет рассчитать рабочие процессы в цилиндре и выпускной системе и определить мощность, развиваемую газовой турбиной.
За один цикл определяется средний адиабатический тепло- перепад в турбине:
 Г ✓ Ч*'1
Г ✓ Ч*'1
 я. = я к
я. = я к
 Т
Т
 ехк-} ех
ехк-} ех
\
где Rex - газовая постоянная смеси газов в выпускном коллекторе.
На каждом шаге расчета в течение цикла рассчитывается скорость изменения мощности турбины:
 dNj _ dGT dcp dcp
dNj _ dGT dcp dcp
Численным интегрированием получаемой таким образом функции dN*r / dcp — f{cp) определяется переменное по углу
поворота кривошипа значение мощности турбины N*T - f(<p). В конце цикла, продолжительность которого по углу определится как (рц-360ту определяется среднее за цикл значение мощ-
ности турбины: NT = 6nNT / срц .
Далее принимается, что мощность компрессора равна мощности турбины (Nfc=NT ). Уравнение для адиабатического напора компрессора записывается в следующем виде:
НК — NTT]K / GK , где г]к - КПД компрессора. Расход воздуха через компрессоры (суммарный) определяется по формуле

где к- показатель адиабаты влажного воздуха.

 Значение Ск определяется в начале расчета рабочего процесса по формуле
Значение Ск определяется в начале расчета рабочего процесса по формуле
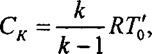
|
где R - газовая постоянная влажного воздуха; Г0' - температура
воздуха на входе в компрессор. Для данного варианта расчета С к считается неизменной.
Давление наддувочного воздуха в ресивере определяется
как ps = р'ъЛКЕ,во, где р'0 - давление воздуха на входе в компрессор; ^во- коэффициент гидравлических потерь в воздухоохладителе. Температура воздуха за компрессором:
Расчет температуры воздуха в ресивере (за охладителем) производится по эмпирической формуле, полученной для теплообменников с большими расходами воды:
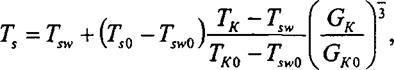
|
где Tsw - температура воды на входе в воздухоохладитель; индексом «0» выделены значения соответствующих параметров на номинальном режиме работы дизеля.
Как уже отмечалось ранее, процесс конденсации паров воды из наддувочного воздуха на трубках воздухоохладителя не рассматривается, хотя его можно легко учесть при наличии опытных данных (см. раздел 1.4).
Для расчета частоты вращения ротора турбокомпрессора использована зависимость


 (6.28)
(6.28)
где Стк- константа; птк - частота вращения ротора турбокомпрессора. Величина Стк определяется путем подстановки в уравнение (6.28) значений T^jiK^rjK^nTK, измеренных для номинального режима работы дизеля. Из формулы (6.28) следует,
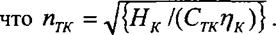
|
Значения 7]т и Т]к, а также коэффициентов гидравлических потерь в реализованном нами алгоритме принимаются по
стоянными, что не вносит существенной погрешности в результаты расчета показателей рабочего процесса даже для долевых режимов работы дизеля.
Алгоритм численного моделирования предусматривает последовательный расчет циклов дизеля, причем результаты расчета предыдущего цикла являются исходными данными для расчета последующего цикла. Это обеспечивает независимость результатов расчета от заданного начального состояния рабочих процессов.
Из рис 6.3 видно, как изменяются некоторые показатели рабочего процесса при расчете пяти последовательных циклов судового дизеля с изобарным наддувом. Показатели а, р5 и в 3-ми 4-м циклах мало отличаются, т. е. их значения установились, и расчет можно было бы завершить. Однако Тех и GK для этих циклов еще существенно отличаются, поэтому расчет надо продолжить, осуществив 5-й цикл. Из приведенного примера ясно, что критерием установления цикла следует принять расход воздуха через компрессор. Практика показывает, что при отличии значений Gk в двух последовательных циклах менее чем на 1,5% расчет можно считать завершенным (в программе для ЭВМ это условие реализуется автоматически). Обычно для достижения установления достаточно трех-пяти последовательных циклов.


 Т еоретически установление может быть достигнуто при любых значениях начальных условий (pSy Т5, рех, Тех и др.), задаваемых в исходных данных для расчета 1-го цикла, однако на практике наличие грубых ошибок в задании начальных условий приводит к тому, что установление становится невозможным. В таком случае значение GK (и других показателей) «раскачивается» от цикла к циклу относительно некоторого среднего уровня, разность значений расхода воздуха при этом вех, время возрастает. В такой ситуации расчет надо прервать и уточнить исходные параметры.
Т еоретически установление может быть достигнуто при любых значениях начальных условий (pSy Т5, рех, Тех и др.), задаваемых в исходных данных для расчета 1-го цикла, однако на практике наличие грубых ошибок в задании начальных условий приводит к тому, что установление становится невозможным. В таком случае значение GK (и других показателей) «раскачивается» от цикла к циклу относительно некоторого среднего уровня, разность значений расхода воздуха при этом вех, время возрастает. В такой ситуации расчет надо прервать и уточнить исходные параметры.
§ 6.7. Интегральные показатели рабочего процесса
После достижения установления определяются итоговые показатели рабочего процесса дизеля (интегральные показатели).
Среднее индикаторное давление pi = Lt / Vh. Индикаторная работа определяется численным интегрированием элементарной работы поршня в течение всего цикла:
_т/ Фи
Z, =—- \p-b d<p.
360 0J
Индикаторная цилиндровая мощность:
К
N. = ——^— р, п. 60пг '
Агрегатная мощность дизеля определяется умножением цилиндровой мощности на число цилиндров.
Удельный индикаторный расход топлива:
g, = 3,672 8ц
РУь 3600
Индикаторный КПД: rji =
SiQM
Доля тепла, отведенного за цикл в охлаждающую среду:
, <Рц
Я. = — JdQw.
StfQ о
Доля тепла, отводимого за цикл с отработавшими газами:
Яг=1~ъ-я*.
Коэффициент избытка воздуха при сгорании:
G’a
а = ——. gyG о
Здесь и далее индекс «а» означает, что показатель определен на момент окончания процесса наполнения рабочего цилиндра. Коэффициент продувки рабочего цилиндра:
G
та
<Ра = —•
V sa а
Суммарный коэффициент избытка воздуха: аг = <расс. Коэффициент наполнения рабочего цилиндра:
RTsGarjsa
=------- —•
PsK
Коэффициент остаточных газов:
Vsa
При задании зависимости для расчета мощности механических потерь для конкретного дизеля определяются также механический КПД и эффективные показатели.
§ 6.8. Примеры использования метода ЧМ
О степени достоверности результатов ЧМ можно судить на основании сравнения экспериментальных данных конкретного двигателя с параметрами, полученными расчетным путем. На рис. 6.4 приведено такое сравнение для судового малооборотного дизеля «Зульцер» 6RTA58 (6ДКРН 58/170). Здесь сплошными линиями показаны данные измерений, выполненных при работе дизеля на стенде завода при его работе по винтовой характеристике. Штриховыми линиями на рисунке отмечены значения показателей, полученные методом численного моделирования на тех же режимах. Расчеты на различных режимах выполнялись при постоянных значениях эмпирических коэффициентов в моделях сгорания топлива, теплообмена и др. Значения этих коэффициентов предварительно были определены на основании сравнения параметров рабочего процесса и данных ЧМ для номинального режима работы дизеля (п ~ 127 об/мин; Ne~ 9560 кВт).
Из рисунка видно, что практически все основные показатели, измеренные на стенде, методом ЧМ определяются с погрешностью не более 3%. Исключение составляет только температура газов на выходе из цилиндра расчетные значения которой во всем диапазоне оборотов выше измеренных на стенде на 40-50°С. В то же время, измеренные значения температуры по штатным приборам после 3-х летнего периода эксплуатации практически полностью совпадают с полученными методом ЧМ.
Математическая модель рабочих процессов, адаптированная к конкретному дизелю в дальнейшем может использоваться для решения широкого круга учебных и исследовательских задач.
В качестве примера рассмотрим результаты, полученные методом ЧМ для этого же дизеля при его работе на винт регулируемого шага при постоянной частоте вращения коленчатого вала (п = 127 об/мин) в диапазоне режимов от полного хода до среднего.
По оси абсцисс на рисунке отложен указатель нагрузки УН (определялся по положению выходного вала регулятора). Для номинального режима УН=8,6 условных делений.
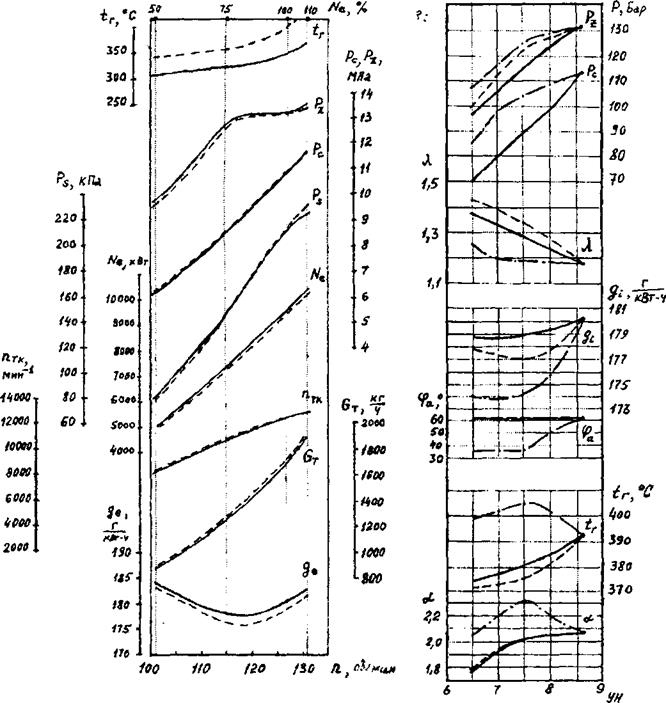 Рис. 6.4. Изменение показателей судового мало- Рис.6.5. К анализу способов
оборотного дизеля «Зульцер» 6RTA58 при работе оптимизации рабочих
по винтовой характеристике:____ по стендовым процессов малооборотного
испытаниям;------ по результатам ЧМ. дизеля
Рис. 6.4. Изменение показателей судового мало- Рис.6.5. К анализу способов
оборотного дизеля «Зульцер» 6RTA58 при работе оптимизации рабочих
по винтовой характеристике:____ по стендовым процессов малооборотного
испытаниям;------ по результатам ЧМ. дизеля
|
Моделирование рабочих процессов проводилось для трех случаев: 1) - работа дизеля без оптимизации рабочего процесса (параметры показаны на рисунке сплошными линиями); 2) - работа дизеля с включенным механизмом VIT (изменение угла опережения подачи топлива в диапазоне нагрузок 70-100%
для поддержания р2 ~ const, показано штриховыми линиями); 3) - работа дизеля с включенным механизмом VEC (изменение угла закрытия выпускного клапана сра для изменения действительной степени сжатия, показано штрих-пунктирными линиями).
Целью оптимизации рабочих процессов является уменьшение удельного расхода топлива на режиме эксплуатационной мощности полного хода (примерно 70-75% от номинала).
Из рис. 6.5. видно, что при действии VIT удельный индикаторный расход снижается примерно на 2 г/(кВт-ч), использование механизма VEC приводит к снижению g, на 6 г/(кВт-ч). Полученные цифры полностью соответствуют экспериментальным данным фирмы «Зульцер».
Недостатком V1T является возрастание жесткости рабочего процесса (характеризуется степенью повышения давления Я = pjpd При использовании VEC наоборот, процесс характеризуется практически неизменным значением А. Вследствие более раннего закрытия выпускного клапана (угол <ра изменялся от 62 до 36° п.к.в. после НМТ) увеличивается действительная степень сжатия, полезный рабочий объем цилиндра. Поэтому растут рс и pz,, свежий заряд воздуха и коэффициент избытка а. Отрицательным моментом является снижение расхода воздуха при продувке цилиндров вследствие уменьшения времени-сечения выпускного клапана и как следствие - возрастание температуры газов за цилиндром, которая определяет теплонапряженность выпускного клапана и газовой турбины.
Расчеты, выполняемые методом ЧМ, называют численным экспериментом. При наличии математической модели можно проводить любые численные эксперименты путем изменения исходных данных по определенному плану. С точки зрения учебного процесса методы ЧМ позволяют глубже изучить взаимосвязь рабочих процессов в цилиндрах, системах газообмена и наддува дизеля.
Глава 7
ОСНОВЫ ДИНАМИКИ ДВИГАТЕЛЕЙ
§ 7.1. Силы и моменты, действующие в кривошипно-шатунном механизме
Основные кинематические соотношения (рис. 7.1). Основными конструктивными параметрами КШМ (кривошипношатунного механизма) являются: радиус кривошипа R и постоянная механизма X- R\L (где L - длина шатуна).
У судовых двигателей величина X лежит в довольно узких пределах - от 0,2 (1/5) до 0,28 (1/3.5), меньшие значения X (от 1/5 до 1/4) относятся к мало- и среднеоборотным двигателям, а большие (от 1/4 до 1/3,5) - к высокооборотным. В малооборотных длинноходных двигателях в связи с увеличением хода поршня резко увеличился радиус мотыля R, что привело к существенному увеличению X - 0,45 (1/2,2) - двигатель S-MC.
Перемещение поршня происходит от ВМТ до НМТ и обратно. Если принять за начало отсчета положение поршня в ВМТ (а = 0°), то проходимый им путь (iS) в функции угла поворота кривошипа а:
S = RU- cosa + XI2sin2a) (7.1), где R - радиус кривошипа.
Скорость поршня (м/с) пропорциональна угловой скорости вала (со= к п /30) и является функцией угла а:
С = Rco ( sin а + X 12 sin 2а) (7.2)
Из формулы (7.2) видно, что изменение скорости поршня подчиняется синусоидальному закону. Так, при а = 0° скорость равна нулю, а при а, близком к 90°, она достигает максимума.
Ее среднее значение за один оборот Cm = 2Sn / 60 = Sn / 30 м / с (7.3), где S - ход поршня, м.
Ускорение поршня, м/с2 а = Ra>2(cosa +Xcos2a), ^ ^ где со - угловая скорость (также переменна).
Максимальные значения ускорение приобретает в мертвых точках поршня, когда скорость его равна нулю; если же скорость достигает максимума, ускорение становится равным нулю.
у KUl/O L/l 4J l/OHCU/ПСЛИ ОПК»*|/уПП^С1/ uci/j/ипил
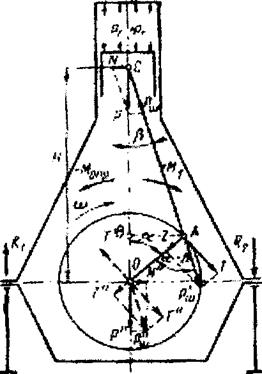 Рис. 7.2. Силы в KLUM, сила Р = Ps+Pj
Рис. 7.2. Силы в KLUM, сила Р = Ps+Pj
|
 Кривошипно-шатунный механизм во время работы двигателя подвергается действию сил давления газов в цилиндре РГ, сил инерции поступательно движущихся масс механизма движения Р,, массы шатунно-поршневой группы, атмосферного давления на поршень со стороны картера и давления наддувочного воздуха в под- поршневой полости цилиндра, трения в звеньях механизма. Последние три силы относительно невелики, и их влиянием можно пренебречь. При рассмотрении оставшихся сил (Рг и Pj) условимся считать их положительными, если они способствуют движению поршня вниз, и отрицательными, если они препятствуют этому движению. На диаграмме сил положительные силы будем откладывать вверх от оси абсцисс, а отрицательные - вниз.
Кривошипно-шатунный механизм во время работы двигателя подвергается действию сил давления газов в цилиндре РГ, сил инерции поступательно движущихся масс механизма движения Р,, массы шатунно-поршневой группы, атмосферного давления на поршень со стороны картера и давления наддувочного воздуха в под- поршневой полости цилиндра, трения в звеньях механизма. Последние три силы относительно невелики, и их влиянием можно пренебречь. При рассмотрении оставшихся сил (Рг и Pj) условимся считать их положительными, если они способствуют движению поршня вниз, и отрицательными, если они препятствуют этому движению. На диаграмме сил положительные силы будем откладывать вверх от оси абсцисс, а отрицательные - вниз.
Сила давления газов (рис. 7.2) приложена к поршню и действует вдоль оси цилиндра. Давление газов рг = Рг/F переменно по значению, закон его изменения определяется из индикаторной диаграммы, перестроенной с применением метода А.Ф. Брикса из координат давление-ход поршня в координаты давление - угол поворота кривошипа (см. рис. 7.3). Для этого проведем полуокружность радиусом R= S/2 от точки О в сторону расположения коленчатого вала (к НМТ) отложим в масштабе чертежа поправку Брикса, см.: 00j = R2 /2L , где L - длина шатуна. Теперь из
точки Оi проведем полуокружность произвольного радиуса. Разделим ее на любое число равных частей (обычно одно деление принимается равным 10 или 15°. Из точки О1через точки деления проведем лучи до пересечения с полуокружностью радиуса R. Проекции точек пересечения на ось абсцисс определяют пути поршня, соответствующие углам поворота кривошипа. Проведя через эти точки вертикали до пересечения с контурами индикаторной диаграммы, найдем значения сил давления газов (рх) соответствующие углам поворота коленчатого вала.
 Полученные данные используются для построения развернутой индикаторной диаграммы в функции угла п.к.в. Длина диаграммы должна соответствовать 720° для 4-х тактных двигателей и 360° для 2-х тактных.
Полученные данные используются для построения развернутой индикаторной диаграммы в функции угла п.к.в. Длина диаграммы должна соответствовать 720° для 4-х тактных двигателей и 360° для 2-х тактных.
Сила инерция поступательно движущихся масс
Эта сила определяется как произведение поступательно движущейся массы Мп на ускорение поршня а, взятое с обратным знаком (так как направление сил обратно направлению ускорений):
Р, = -Мпа(1.5),
где М„ = Gn /g масса поступательно движущихся частей, кг; Gn - суммарный вес поступательно движущихся частей, g- = 9,81 — ускорение свободного падения м/с2.
Суммарный вес поступательно-движущихся частей Gn складывается из веса комплекта поршня Gnop и веса части шатуна Gujn• В крейцкопфных двигателях к Gn относят также вес штока и крейцкопфа Grp.
Таким образом: Gn = Gnop + Gmn + GKP., где Gum = 0,4Gui - часть веса шатуна, участвующая в поступа
тельном движении. Остальная часть Gwb = 0,6 Gm участвует во вращательном движении.
Для удобства дальнейших расчетов в уравнения сил инерции вводим массу, отнесенную к площади поршня тп = Мп/ Fn. Это дает возможность силы инерции привести к одной размерности с давлением газов.
После замены ускорения а в формуле (7.5) на его выражение из (7.4) получим:
Pj = - тп Rco2 ( cos а + Xcos2a) (7.6)
Как видно из полученного выражения, сила инерции Pj, как и Рг, переменна и зависит от угла поворота кривошипа. Она приложена к центру головного соединения и направлена по оси цилиндра.
 Задаваясь рядом значений а, можно определить мгновенные значения силы инерции и по ним построить кривую сил инерции (рис. 7.4). Более удобным является графический способ, описание которого можно найти в методических руководствах по расчету двигателей.
Задаваясь рядом значений а, можно определить мгновенные значения силы инерции и по ним построить кривую сил инерции (рис. 7.4). Более удобным является графический способ, описание которого можно найти в методических руководствах по расчету двигателей.
Дата добавления: 2016-05-16; просмотров: 938;
