ОСНОВЫ ТЕОРИИ РАБОЧИХ ПРОЦЕССОВ В ЦИЛИНДРЕ ДИЗЕЛЯ § 1.1. Идеальный цикл дизеля 12 страница
С учетом приведенных выше зависимостей: V = Vc + Vh а /2. Так как объем камеры сжатия не всегда известен, можно ис
пользовать следующую зависимость:
 Г ^ \
Г ^ \
(6-8)
------------ К CL
\ £0 ~ 1 J
где £0 — геометрическая (номинальная) степень сжатия. Продифференцировав уравнение (6.8), получим:
dV = -^——bdtp, (6.9)
180 2
где Ъ = sin <р{ 1 + Яш cos (р) - тригонометрическая функция, именуемая аналогом скорости поршня. Коэффициент 7г/180 веден в уравнение (6.9) в связи с переводом угла поворота коленчатого вала из радиан в градусы.
Разделив уравнение (6.7) на ^ и учитывая, что энтальпии
газовin =ип+ p„vn;im -ит+ pmvm, получим дифференциальное
уравнение первого закона термодинамики в окончательном виде:

 dT 1 dgx dQ dG nVh . dG„ . dGn л QH-TL+~^-cJ—-T±pb^n-rL-h
dT 1 dgx dQ dG nVh . dG„ . dGn л QH-TL+~^-cJ—-T±pb^n-rL-h
состояния рабочего тела, определим кривую изменения давления газов в цилиндре (т. е. индикаторную диаграмму), что и является конечной целью процесса численного моделирования.
Уравнение состояния применительно к внутрицилиндро- вым процессам запишется так: pV = GRT' откуда
GRT
р=—> (б-п> где R - газовая постоянная смеси, кДж/(кг*К).
Численное решение уравнений (6.10) и (6.11) предполагает детальную расшифровку отдельных членов, входящих в их правые части. Эти члены сами являются сложными функциями угла поворота коленчатого вала двигателя, поэтому рассмотрим каждый из них отдельно.
§ 6.2. Математическая модель сгорания топлива в цилиндре дизеля
Первое слагаемое в правой части уравнения (6.10) QH{dgx!d(p) представляет собой скорость выделения тепла при сгорании топлива, кДж/(°п.к.в.) В свою очередь, dgjdcp называют скоростью сгорания топлива, кг/(°п.к.в.). Текущую массу сгоревшего топлива gx можно представить как gx = g^x, где g4 - цикловая подача топлива, кг/цикл; х = gx !gM - относительное количество сгоревшего топлива. Очевидно, что х изменяется от нуля в начале процесса сгорания до 1 в его конце (полагаем, что топливо сгорает полностью). Первая производная от х по углу поворота коленчатого вала dx!d(p называется относительной скоростью сгорания топлива и имеет размерность 1/(°п.к.в.).
Зависимости dx/d(p = fi(cp) и х = f2((p) часто называют законом сгорания топлива, записанным в дифференциальной и интегральной формах соответственно. Сгорание топлива в значительной мере зависит от «закона» его подачи в цилиндр gj =f((p), где gr - масса впрыснутого в цилиндр топлива. По аналогии со сгоранием топлива введем понятие дифференциальной и интегральной характеристик впрыска топлива daldcp = fi((p) и а = f4<p)'
Здесь а = gr/gM - относительная масса впрыснутого топлива. Характеристики впрыска определяются, главным образом, формой кривой давления топлива перед распылителем форсунки. Протекание процессов впрыска и сгорания топлива существенно зависят от закона подачи топлива.
В настоящее время используется широкая гамма математических моделей процесса сгорания. В простейших из них переход от характеристики впрыска к характеристике сгорания осуществляется непосредственно, минуя промежуточные стадии физико-химических превращений. В самых сложных в той или иной мере используются общие законы тепло- и массообмена, диффузии, химической кинетики. Разработаны многомерные модели нестационарной топливной струи с учетом теории турбулентного горения и термодинамики многокомпонентных сред.
Однако ввиду чрезвычайной сложности применения физико-химических законов к процессам смесеобразования и сгорания в условиях дизеля эти методы также включают ряд коэффициентов, подлежащих определению экспериментальным путем. Разработаны и модели среднего уровня сложности, доведенные до рабочих программ ЭВМ, например метод, разработанный Н.Ф. Разлейцевым для моделирования и оптимизации процесса сгорания в тепловозных дизелях.
 В инженерной и исследовательской практике чаще всего используются наиболее простые модели сгорания, позволяющие экономить время счета ЭВМ. Хорошее соответствие опытных и расчетных данных достигается путем выбора коэффициентов в уравнениях, описывающих характеристики сгорания. Большое распространение получила формула И.И. Вибе, которая имеет вид
В инженерной и исследовательской практике чаще всего используются наиболее простые модели сгорания, позволяющие экономить время счета ЭВМ. Хорошее соответствие опытных и расчетных данных достигается путем выбора коэффициентов в уравнениях, описывающих характеристики сгорания. Большое распространение получила формула И.И. Вибе, которая имеет вид
(6.12)
где (pz - условная продолжительность сгорания топлива; т - показатель характера процесса сгорания.
Используются также формулы других авторов, именуемые «эмпирическими». Большим недостатком этих формул является то, что они не учитывают характеристику впрыска топлива.
Кроме того, эмпирические формулы носят частный характер и не могут применяться при моделировании рабочих процессов дизелей других типов без предварительных исследований.
При моделировании рабочих процессов судовых средне- и малооборотных дизелей используется метод расчета характеристик сгорания, разработанный автором в середине 70-х годов. По уровню сложности алгоритма метод близок к эмпирическим формулам, в то же время он более физично описывает основные закономерности сгорания в дизеле.
 В этом методе между а их введена промежуточная функция w =fs(<p), отражающая динамику подготовки топлива к сгоранию. Параметр w = gjg4 представляет собой текущее относительное количество подготовленного к сгоранию топлива. Полагаем, что подготовленное к сгоранию топливо связывает воздух в объеме факела стехиометрическим соотношением. Положив также, что скорость протекания физических процессов пропорциональна общей текущей поверхности капель распыленного топлива, запишем уравнение для относительной скорости подготовки топлива к сгоранию в следующем виде:
В этом методе между а их введена промежуточная функция w =fs(<p), отражающая динамику подготовки топлива к сгоранию. Параметр w = gjg4 представляет собой текущее относительное количество подготовленного к сгоранию топлива. Полагаем, что подготовленное к сгоранию топливо связывает воздух в объеме факела стехиометрическим соотношением. Положив также, что скорость протекания физических процессов пропорциональна общей текущей поверхности капель распыленного топлива, запишем уравнение для относительной скорости подготовки топлива к сгоранию в следующем виде:

 (6.13)
(6.13)
величина, пропорциональная суммарной
поверхности капель топлива в камере сгорания; у = f6((p) - корректирующая функция.
В уравнении (6.13) использованы также следующие обозначения: х “ эмпирический показатель, учитывающий степень
неравномерности распыливания топлива; при абсолютно равномерном распыливании (все капли имеют одинаковый диаметр) X = 2/3, при неравномерном распыливании х = 0.8-1,0.
На основе анализа экспериментальных характеристик сгорания в дизелях различных типов при их работе в широком диапазоне нагрузочных и скоростных режимов получена следующая эмпирическая формула для описания корректирующей функции в уравнении (6.13):
„ 1 f 0,62574190 Y у = В
 р{ 273 J
р{ 273 J
Структурно формула (6.14) состоит из трех комплексов. Первый из них
1 f 0,62574190 V р{ 273 J
отражает влияние параметров рабочего тела в цилиндре на скорость взаимодиффузии паров топлива и воздуха в камере сгорания. По ходу процесса этот комплекс численно возрастает. Второй комплекс выражается зависимостью
a-w
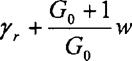
|
и отражает снижение скорости подготовки топлива к сгоранию по мере роста концентрации подготовленного топлива и снижение массы «чистого» воздуха в среднем по объему камеры сгорания.
В связи с тем, что в смесеобразовании участвует не весь воздушный заряд, а только часть его, необходимо учесть динамику развития топливных факелов. С этой целью использована экспоненциальная зависимость
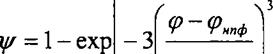
|
(6.15)
представляющая собой третий комплекс. Здесь (рнпф - угол начала подачи топлива форсункой; (рф - условная продолжительность развития топливных факелов в камере сгорания. Величина срф определяет темп возрастания и положение максимума скорости сгорания. При больших (рф скорость сгорания растет медленнее, а ее максимум смещается к окончанию впрыска и наоборот.
Формула (6.14) также содержит коэффициент пропорциональности В, который учитывает физические свойства топлива, газодинамические условия в камере сгорания, мелкость распы- ливания топлива и другие факторы. В силу многофакторности его выбор возможен только на основе сопоставления (идентификации) расчетных характеристик сгорания с экспериментальными характеристиками. С увеличением В максимум скорости сгорания возрастает, продолжительность сгорания сокращается.
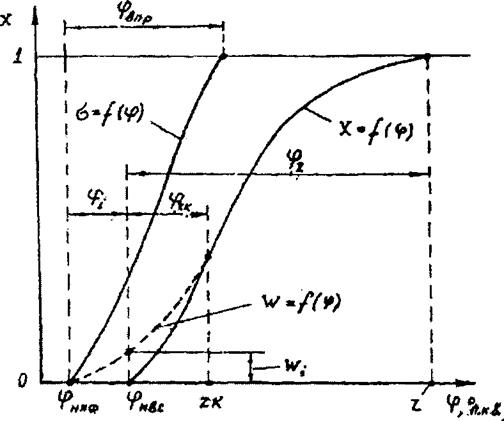 Рис. 6.1. Характеристики впрыска, подготовки и сгорания топлива
Рис. 6.1. Характеристики впрыска, подготовки и сгорания топлива
|
Схема расчета характеристик сгорания иллюстрируется рис. 6.1. Момент начала подачи топлива <рнпф и характеристика впрыска должны быть заданы в исходных данных. Относительная скорость подготовки к сгоранию рассчитывается по уравнению (6.13) с учетом зависимостей (6.14) и (6.15) на протяжении всех периодов процесса сгорания. Расчет dw/dcp ведется совместно с уравнениями (6.10) и (6.11), отражающими изменение параметров рабочего тела в цилиндре. Текущее количество подготовленного к сгоранию топлива определяется интегрированием уравнения (6.13) на каждом шаге счета.
Период задержки самовоспламенения может быть рассчитан по одной из эмпирических формул. Для судовых дизелей используется формула
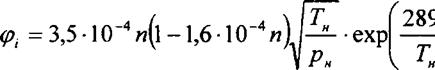
|
| Л -0,04ЦЧ ,(6.16) |
где рн, Тн - давление и температура газов в цилиндре в момент начала подачи топлива; ЦЧ- цетановое число топлива.
Формула (6.16) получена из зависимости А.И.Толстова для периода задержки самовоспламенения и дополнена экспоненциальной функцией, приближенно отражающей влияние на це- танового числа.
Момент начала сгорания <рнвс определяется как сумма (Рнвс - <рнпф + (pi• В точке начала видимого сгорания (НВС) фиксируется относительное количество топлива, подготовленного к сгоранию за первую фазу процесса, w* = gwi/gu• После воспламенения доля топлива w, сгорает по кинетическому механизму. Расчет характеристик сгорания этой части топлива осуществляется по уравнению И.И. Вибе, записанному в виде
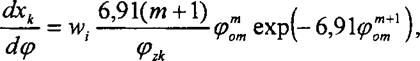
|
где dxj/dcp - кинетическая составляющая скорости сгорания; срл- условная продолжительность сгорания топлива по кинетическому механизму (т. е. продолжительность фазы быстрого сгорания топлива - второй фазы процесса сгорания); m - показатель характера сгорания; (pom » ((p-<pHec)/<Pzk - относительное изменение угла поворота коленчатого вала.
Допускаем, что после начала сгорания подготавливаемое топливо мгновенно воспламеняется и сгорает. Таким образом, вторая (диффузионная) составляющая относительной скорости сгорания, существующая с момента НВС и до конца сгорания в точке z (т. е. в течение третьей фазы процесса сгорания), приравнивается к dw/d<p.
На участке от НВС до zk скорость сгорания определяется как сумма двух составляющих:
dx dxt dw
— 1 .
d(p dcp d(p
После выгорания w. dxk / dip = 0, поэтому с данного момента и до конца сгорания dx! dcp = dw I dcp.
Относительное количество сгоревшего топлива вычисляется путем численного интегрирования дифференциального уравнения для скорости сгорания.
Рассматриваемая методика позволяет рассчитать характеристики сгорания при различных законах подачи топлива, в том числе при ступенчатом или двойном впрыске, так как
а = /4 {<р) является исходной функцией, трансформируемой посредством переходной функции w = f5 ((р) в конечную x~fi (Ф) > как показано на рис. 6.1.
Величины настроечных параметров В9<Рф^т^<рА^х^ как
уже отмечалось, определяем путем идентификации расчетных и экспериментальных характеристик сгорания.
Опыт расчетов для судовых дизелей показывает, что параметр В лежит в пределах 0,15-0,35. Столь широкий диапазон обусловлен тем, что в этом параметре сконцентрирован учет большого числа факторов, не получивших отражения в математической модели сгорания.
Параметр (рф можно определить из установленного диапазона (рф / <рн = 0,3 -г- 0,8, где (рнтр - продолжительность впрыска топлива на номинальном режиме.
Показатель % для всех исследованных типов дизелей принимался равным 0,9. Значения <рА лежат в пределах 10-20° п.к.в.
Точная идентификация этого параметра возможна лишь в дизелях, имеющих два максимума скорости сгорания (параметры т
и ^величину и положение первого максимума). В судовых
дизелях в силу высокой управляемости процесса сгорания за период задержки самовоспламенения к сгоранию успевает под
готовиться не более 10% цикловой подачи топлива, поэтому точность определения т и (pzk мало отражается на расчете характеристик сгорания в целом. Однако для долевых режимов работы доля подготовленного топлива wt значительно возрастает, и роль параметров тифж становится более существенной.
§ 6.3. Расчет теплообмена со стенками цилиндра
Расчет процесса теплообмена в цилиндре является не менее сложной задачей, чем расчет сгорания топлива. Однако погрешность в определении количества теплоты, отводимой в стенки цилиндра, значительно меньше отражается на итоге расчета - индикаторной диаграмме и основных показателях работы дизеля. Это объясняется тем, что доля тепла, отводимая в стенки цилиндра, составляет в современных дизелях 8-15% от выделившегося тепла при сгорании цикловой подачи топлива.
В упрощенной методике расчета теплоообмена количество теплоты, отводимой от газов к стенкам цилиндра, находится из уравнения Ньютона-Рихмана, которое в дифференциальной форме записывается следующим образом:
dQw=a!Fx(Tw-T)dr,
где аг - коэффициент теплоотдачи от газов к стенкам; Fx - текущая поверхность теплообмена; Tw - средняя условная температура стенок; т - время теплообмена.
 При постоянной частоте вращения коленчатого вала двигателя d(p = 6nr, поэтому dr = dq)l(6n\ С учетом последней зависимости преобразуем уравнение теплообмена к виду
При постоянной частоте вращения коленчатого вала двигателя d(p = 6nr, поэтому dr = dq)l(6n\ С учетом последней зависимости преобразуем уравнение теплообмена к виду
= 7-<*,FX(TW-T). (6.17)
Ьп
Уравнение (6.17) представляет скорость теплообмена между газами и стенками цилиндра - второе слагаемое правой части дифференциального уравнения (6.10).
Величина Fx включает в себя постоянную поверхность камеры сгорания и переменную величину поверхности цилиндро
вой втулки, открываемую (закрываемую) при перемещении поршня. Учитывая формулы, приведенные для Sx в разделе 6.1, запишем:
 ~1 if 2 Л —I—--- ь а
~1 if 2 Л —I—--- ь а
S D{Ј0 -1 J
где D - диаметр цилиндра.
Для расчета dQw/ d(p необходимо определить аг. В рассматриваемой методике для этой цели используется формула Эйхельберга:
аг=С3 \[С^'у[рТ> (6-18)
где Сэ - эмпирический коэффициент; Ст - Sn/ЗО - средняя скорость поршня, м/с.
Средняя условная температура стенок цилиндра в уравнении (6.17) представляет собой постоянную, осредненную по поверхности теплообмена и времени температуру, которая дает при расчете величину теплоотдачи в охлаждающую среду за цикл, равную величине теплоотдачи, полученной опытным путем.
Величина Tw может быть рассчитана, если известны: доля тепла, отводимого в стенки цилиндра, средняя толщина и коэффициент теплопроводности материала стенок, коэффициент теплоотдачи от стенок в охлаждающую жидкость и температура жидкости.
Расчеты показывают, что Tw изменяется в довольно узких пределах для дизелей различного класса: для номинального режима Tw = 450-520 К; для долевых режимов в зависимости от нагрузки и типа дизеля Tw = 350-450 К. Ошибка в задании Tw на 100 К приводит к погрешности расчета величины Qw примерно 10%, погрешность расчетной индикаторной работы и производных от нее показателей работы дизеля не превышает при этом 2%.
В связи с определенными трудностями в подборе исходных данных для расчета Tw в тех случаях, когда не требуется исследовать собственно процесс теплообмена, величину Tw можно выбирать в соответствии с указанными выше пределами. При
этом следует иметь в виду, что большие значения Tw характерны для высокофорсированных дизелей.
Коэффициент пропорциональности Сэ в уравнении (6.18) для судовых дизелей лежит в пределах 1,5-2,5. Меньшие его значения характерны для сверхдлинноходных малооборотных судовых дизелей, у которых доля тепла, отводимого в охлаждающую среду, составляет 8-10 %. Верхний диапазон Сэ=2,0-2,5 характерен для среднеоборотных четырехтактных дизелей с долей отводимого в охлаждающую среду тепла 15-20 %. Точное определение Сэ возможно путем проведения пробных расчетов и сопоставления расчетного значения Qw данным теплобалансовых испытаний дизеля.
§ 6.4. Уравнения массового баланса
В большинстве известных замкнутых численных моделей рабочих процессов дизелей рассматривается двухкомпонентная смесь газов, состоящая из воздуха и чистых продуктов сгорания (см. раздел 1.5).
Исследования показывают, что для судовых дизелей, часто эксплуатирующихся в климатических зонах с высокими температурой и влажностью атмосферного воздуха, необходимо учитывать наличие водяного пара в свежем заряде. Кроме того, водяной пар как компонент газовой смеси в цилиндре добавляется к рабочему телу в значительно больших количествах при применении специальных методов для снижения образования оксидов азота: работе двигателя на водотопливной эмульсии, при непосредственном впрыске воды в камеру сгорания или увлажнении надувочного воздуха (подробно об этом см. главу 15).
В соответствии с отмеченным положим, что в любой момент времени масса рабочего тела в цилиндре состоит из трех компонентов: G = G' + Grr + Gnt, где G\Gn,Gm- массы сухого
воздуха, чистых продуктов сгорания и водяного пара соответственно. Разделив обе части последнего уравнения на М9 получим:
r4r4rw = l,rfle r' = G’IG\rtf = G”IG\rm = GmIG - массовые доли сухого воздуха, чистых продуктов сгорания и водяного пара в смеси газов.
В течение рабочего цикла изменение массы рабочего тела вызвано: сгоранием топлива (приращение массы равно g^x); поступлением продувочного воздуха в цилиндр и удалением из него отработавших газов в период газообмена. При сгорании топлива масса воздуха уменьшается на величину Gog^x, а масса чистых продуктов сгорания увеличивается на величину
(с0+1к,*-
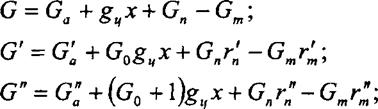
|
| Законы сохранения массы (уравнения массового баланса) записываются следующим образом: |
| (6.19) |
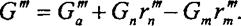
|
Состав смеси газов в начале сжатия Ga = G'a + Gna + G™
определяется с учетом влагосодержания атмосферного воздуха и остаточных газов в цилиндре. Кроме известных в уравнениях массового баланса используются следующие обозначения: г'п , rfг'"п> - массовые доли сухого воздуха, чистых продуктов сгорания и водяного пара в смеси газов, поступающих в цилиндр через впускные органы (г „+ r"n + rmn = 1); г'т, г”т, г,п т - то же Для смеси газов, удаляемых из цилиндра через выпускные орга-
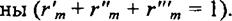
|
Атмосферный воздух, поступающий в систему воздухо- снабжения, содержит 1/(1 +d) часть сухого воздуха и d/(\+d) водяного пара. Большая часть водяного пара поступает в цилиндр, меньшая - конденсируется на трубках воздухоохладителя, задерживается во влагосборнике и удаляется из него в льяла или специальную емкость при периодических продуваниях (см. раздел 1.4).
Дифференциальное уравнение (6.10) помимо текущих значений масс газов включает в себя также скорости их изменения по углу поворота коленчатого вала, поэтому с учетом выраже
ний (6.19) запишем систему уравнений массового баланса в дифференциальной форме:
dG dx dG dGm
----- — g----------- 1------ 2---------- 2L;
 dcp 4 dip dcp dcp
dcp 4 dip dcp dcp
_____ m
m
dcp " 4 dcp " dcp dcp dG _(q , i \ dx „ dGn „ dGm
—— - (Cr0 + i )g — + Г„ — Гт ——
dcp dcp dcp dcp
dGm JGn dGm
n i m
d(p d(p d(p
При моделировании рабочего процесса на влажном воздухе необходимо задать величину влагосодержания d. В том случае, если моделируется работа дизеля на водотопливной эмульсии или с непосредственным впрыском воды в цилиндр, в уравнения массового баланса для водяного пара нужно добавить соответствующие члены. Кроме того, в уравнение (6.10) также необходимо добавить члены, учитывающие потерю тепла на испарение воды.
Расходы газов через органы газораспределения определяются по уравнению истечения установившегося потока с использованием упрощенной зависимости
dG: - “
— = 0,23645 I— 1 -£2- (6.20)
 dcp Jrtx ’ va
dcp Jrtx ’ va
где Gj = Gn для впускных органов, G. = Gm - для выпускных; /- проходное сечение органов газораспределения; ju - коэффициент расхода; рх, 7J - давление и температура в потоке газов перед проходным сечением; р\ - условное давление за проходным сечением; R - газовая постоянная; со = тг/30- угловая скорость коленчатого вала дизеля.
Текущие массы газов, поступающих в цилиндр и уходящих из него в процессе газообмена, определяются численным интег
рированием дифференциальных уравнений, записанных на основе зависимости (6.20) отдельно для впускных и выпускных органов.
Величина р2 определяется в зависимости от соотношения
Рг ^ Р\ ’ гДе ~ реальное давление за проходным сечением. Из
теории ДВС известно, что величина критического отношения давлений выражается формулой
к-1
 , где к = с _ / с - показатель адиабаты.
, где к = с _ / с - показатель адиабаты.
\к + 1 j
кр
Если р2 / рх <Ркр принимается р’2 = Ркрр2 (надкритическое
истечение); при докритическом истеченииpr2 = Р2 •
В реализованном нами алгоритме газообмен рассчитывается при переменных R и /г, определяемых по тем же формулам, что и для участков сжатия, сгорания и расширения. Для фазы продувки рассчитывается обратное истечение (заброс) газов из цилиндра в продувочный ресивер, если складывается обратное нормальному соотношение давлений.
Геометрические проходные сечения органов газораспределения задаются в табличной (или в иной) форме в зависимости от угла поворота коленчатого вала. Коэффициенты расхода ориентировочно принимаются по литературным данным, а затем уточняются в процессе идентификации численной модели дизеля.
Допущение о равенстве температур и компонентов газовой смеси в каждой точке рабочего цилиндра становится неверным для участка газообмена, так как при продувке (особенно в двухтактных дизелях) эти параметры существенно отличаются по объему цилиндра. В упрощенных математических моделях предполагается двухстадийный характер взаимодействия продувочного воздуха с газами в цилиндре. Считается, что в начале продувки продувочный воздух, поступая в цилиндр, не смешивается с газами. Обычно полагают, что разделяющая поверхность непроницаема для теплоты и вещества, но абсолютно эластична, т. е. в объеме цилиндра соблюдается механическое рав
новесие (давление одинаково), однако температура и состав газов в зонах различны.
Такое допущение позволяет с начала свободного выпуска и до некоторого момента в фазе принудительного выпуска - продувки принимать, что через выпускные органы в выпускной коллектор удаляются только отработавшие газы, состав которых определяется соотношениями: г' т = г'; г”т = г"; г"’т= г”\ Температура этих (остаточных) газов определяется по уравнению сохранения энергии, записанному для зоны. Давление газов в зоне равно текущему давлению в цилиндре, рассчитываемому по уравнению состояния (6.11), в котором аргументом является текущая среднемассовая температура рабочего тела в цилиндре.
Для конца продувки принимают гипотезу полного перемешивания газов. Она предполагает, что продувочный воздух образует однородную смесь с газами, находящимися в цилиндре, поэтому в каждой точке объема цилиндра давление, температура и концентрации компонентов одинаковы.
В реальных процессах полного перемешивания не происходит, поэтому в математической модели для заключительной стадии необходимо задать закон перехода от послойного вытеснения к полному перемешиванию.

 В реализованной нами методике этот закон определяется задаваемой в исходных данных экспериментальной кривой
В реализованной нами методике этот закон определяется задаваемой в исходных данных экспериментальной кривой
7, =/(?,). где JJS=G'/G -
КПД продувки (коэффициент очистки цилиндра); <ps -GJG - коэффициент
 избытка продувочного воздуха. Эта зависимость (закон очистки) приведена на рис.6.1.
избытка продувочного воздуха. Эта зависимость (закон очистки) приведена на рис.6.1.
Линия 1 соответствует гипотезе послойного вытес
нения. До момента, отмеченного точкой а на линии У, имеем равенство Т]5 = (р5. Это означает, что весь воздух, поступающий
через впускные органы, остается в цилиндре (G = GJ. Как уже отмечалось, на этом участке в выпускной коллектор удаляются только газы. После точки Ъ в выпускной тракт начинает поступать только продувочный воздух. Линией 1 можно аппроксимировать схему очистки четырехтактного дизеля.
Кривая 2 соответствует опытному закону очистки цилиндра судовых малооборотных дизелей с прямоточно-клапанным газообменом. До точки а эта кривая совпадает с линией 7, а затем отклоняется вниз. Правее точки a Tjs < cps , а это означает,
что часть воздуха начинает уходить в выпускной тракт вследствие частичного перемешивания с газами. Для дизелей с контурными схемами газообмена точка а располагается левее, а кривая смещена ниже.
Состав отработавших газов и их температура для заключительной фазы продувки цилиндра определяются на основе заданного закона очистки цилиндра.
§ 6.5. Расчет теплоемкостей, газовых постоянных и теоретической массы воздуха
В численных моделях рабочих процессов ДВС принято пользоваться табличными данными для вычисления истинных изохорных теплоемкостей воздуха и чистых продуктов сгорания. В упрощенных алгоритмах вместо таблиц используют аппроксимирующие зависимости, типа cv = а + ЪТ + с/7*, где а, Ь, с - постоянные коэффициенты. Как уже отмечалось, влагосодержание воздуха при этом не учитывается.
Расчет теплоемкости чистых продуктов сгорания осуществляется по аппроксимирующей зависимости с коэффициентами а, Ь, с, определенными для углеводородного топлива среднего состава С = 0,87; Н = 0,126; О = 0,004 при стехиометрическом соотношении воздух/топливо.
Дата добавления: 2016-05-16; просмотров: 943;
