ОСНОВЫ ТЕОРИИ РАБОЧИХ ПРОЦЕССОВ В ЦИЛИНДРЕ ДИЗЕЛЯ § 1.1. Идеальный цикл дизеля 14 страница

Рис. 7.4. Развернутая диаграмма СИЛ Р₃, PjV\P

Суммарная сила Р представляет собой алгебраическую сумму сил действия газов Р_Г и инерции поступательно движу­щихся масс Pj. Кривая этой силы, характеризующая ее изменение в течение цикла, может быть получена путем суммирования ординат кривых Рг и Pj с учетом их знака, построенных для двухтактного двигателя на базе 360° п. к. в. (см. рис. 7.4) и для четырехтактного на базе 720° п. к.в.¹

Суммарная с и л а Р, как и ее составляющие, прило­жена к центру головного соединения и действует вдоль оси ци-

⁵ Здесь и далее силы Р, R,N,T,Z приняты условно, так как фактически они при­ведены к единице площади поршня и имеют размерность Н/м².

линдра. Она может быть разложена на две составляющие (рис. 7.2): силу, действующую по оси шатуна, Р_ш ~ P/cos/З, и силу, перпендикулярную оси цилиндра, N = Р / tg/3.

Если принять tg/i = sinp ввиду малости угла и, поскольку sin ft = X sina (из рассмотрения треугольников САВ и ОБА), то

N = PXsina . (7.7)

Сила N (нормальная сила) прижимает трон- ковую часть поршня к стенке цилиндра (в тронковом двигателе) или ползун крейцкопфа к его направляющей (в крейцкопфном двигателе). Сила переменна по направлению, этим объясняется происходящая при работе двигателя перекладка поршня и пол­зуна крейцкопфа с борта на борт.

Сила Р_{ш t} действующая по оси шатуна, сжимает его стер­жень. Перенесем силу Рш по линии ее действия в центр криво­шипной шейки (точка А) и разложим ее на две составляющие: Тангенциальную силу, касательную к окружности, описанной радиусом R,

T-P„_Sm(a+/l>=P^{SHa + /3>}

COS Р

и радиальную силу, направленную по радиусу кри­вошипа, Z = Рц/cos (а + Р) = Р Cos Д (7.9)

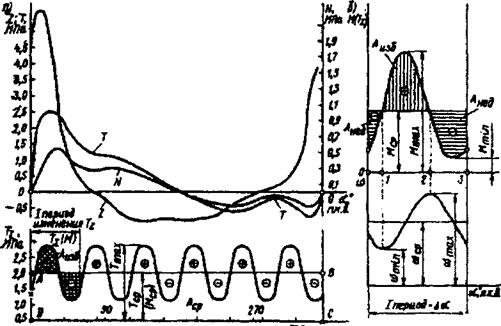« * т то т до т Рис. 7.5. Кривые сил: нормальной N, радиальной Z и тангенциальных Т и Tz для 2-х тактного двигателя

На основании выражений (7.7)-(7.9) можно построить кри­вые N, Z и Т в функции угла поворота кривошипа (рис. 7.5). Нормальная, радиальная и тангенциальная силы непостоянны и в пределах каждого рабочего цикла принимают как положитель­ные, так и отрицательные значения. Отсюда переменны и вызы­ваемые ими нагрузки в элементах конструкции двигателей.

Крутящий и опрокидывающий моменты

Перенесем радиальную силу Z (см. рис. 7.2) по направле­нию ее действия в центр коленчатого вала О и приложим одно­временно к центру вала две взаимно противоположные и равные силы Т и Г" параллельные и равные в свою очередь тангенци­альной силе Т. Силы Т и Т образуют пару сил (с плечом R), мо­мент которой, называемый крутящим моментом, приводит во вращение коленчатый вал:

М_ц= TFnR =Р ^S1-^{a +}/-- F_nR , (7.10)

cos (5

где Fn - площадь поршня (в формулу включена в связи с тем, что сила Р относится к 1 см² площади поршня).

Поскольку тангенциальная сила непостоянна, то изменяется и вызываемый ею крутящий момент. Кривую Т (см. рис.7.5) на основании выражения (7.10) можно рассматривать и как кривую Мц одного цилиндра, только масштаб оси ординат будет иным. Сложение сил Z" и Т" (см. рис. 12) дает равнодействующую си­лу Р"ш, нагружающую рамовые подшипники коленчатого вала.

Pin” ~ Рш ~ Рш — Р / COS0

Разложим силу Р"ш на две составляющие - горизонталь­ную N"и вертикальную Р”:

Р" = Р"_ШС05р = (Р / cosp) . cos/i - Р N" = P"insinfi = (jP /cosp) . sin/i ~P tg/3 = N, напомним, что sin/i « tgp

Равные по значению силы N и N" передаются остову двига­теля и образуют пару сил с плечом Н. Эта пара сил стремится по­вернуть двигатель вокруг продольной оси в сторону, противопо­ложную вращению коленчатого вала. Создаваемый ими момент называется опрокидывающим моментом, (Нм)

М_опр= -NF_nH, (7.11) который численно равен крутящему моменту М_ц, но направлен в противоположную сторону: М_опр = - Мц, (см. рис.7.2).

Опрокидывающий момент, будучи приложенным к остову двигателя, передается опорам фундамента, вызывая в них реакции Rj и R₂, которые могут быть определены из равенства внешнего реактивного момента:

M_R = Rj,₂ 1ф = М_опр, откуда Rj₂ = М_опр/ 1_Ф, (7.12)

где 1ф - расстояние между опорами, м.

Таким образом, фундамент двигателя испытывает дейст­вие периодически меняющейся силы инерции поступательно дви­жущихся масс, воспринимает переменный опрокидывающий мо­мент и нагружается весом двигателя.

До сих пор рассматривались силы и моменты, возникаю­щие в пределах одного цилиндра. В многоцилиндровом двига­теле коленчатый вал воспринимает и передает суммарный кру­тящий момент всех цилиндров, мгновенные значения которого

М = TzF_nR, (7.13) где Tz - мгновенное суммарное касательное усилие (см. рис.7.5*), условно приложенное к фланцу коленчатого вала на радиусе R

Для нахождения усилия Tz необходимо суммировать через 10-15° значения сил Г всех цилиндров. На основе полу­ченных данных строят кривую Tz=f (а).

Для многоцилиндрового двигателя эта кривая представляет собой периодическую функцию с периодом, равным углу закли­нивания кривошипов вала. Планиметрирование площади под ней на протяжении одного периода позволяет установить среднюю тангенциальную силу, равную отношению площади к длине од­ного периода и определяющую средний крутящий момент дви­гателя, Нм,

М_ср = T_cpF_nR (7.14)

N.

ишМср — 9550—^L, (7.15)

п

где Ni - мощность двигателя, кВт; п - частота его вращения, 1/мин.

§ 7.2. Неравномерность вращения вала

Крутящий момент двигателя, как и составляющие моменты отдельных цилиндров, непостоянен и представляет собой перио­дическую функцию с периодом изменения, равным углу заклини­вания кривошипов А а (см. рис.7.5, а, б). Наряду с этим момент, поглощаемый гребным винтом или генератором М_п,_эи , практи­чески постоянен и на установившемся режиме должен быть равен среднему крутящему моменту двигателя

Мп.эн ⁼ М_Ср. На диаграмме 7^(а) (см. рис.7.5, а) средняя величина момента М_Ср представлена в виде прямой, проведен­ной параллельно оси абсцисс на расстоянии от нее, равном Тср.

Площадь прямоугольника ABCD, построенного на базе 0-360° п. к. в. с ординатой Т_ср, будет представлять собой сред­нюю работу А_ср крутящего момента. Если рассматривать измене­ние момента двигателя М (Т£) относительно поглощаемого мо­мента М_ср (Т_ср), то (см. рис.7.5, а, б) в отдельные периоды разви­ваемый двигателем момент превышает момент, потребляемый гребным винтом или иным потребителем энергии (М > М_ср), или Tz^> Т_ср> а в другие периоды момент двигателя меньше поглощае­мого момента.

В соответствии с этим и работа крутящего момента двига­теля то больше его среднего значения, то меньше. Так, на участ­ке 0-1 (см. рис. 7.5, б) работа отрицательная (А_нед). Недостаток работы восполняется путем использования части кинетической энергии вращающихся масс двигателя и гребного винта. При этом угловая скорость вала со падает. На следующем участке 1-2 работа положительная; избыточная работа А_Шб расходуется на увеличение кинетической энергии вращающихся масс, и угловая скорость повышается. На участке 2-3 снова недостаток энер­гии, и угловая скорость снижается.

Колебание частоты вращения вала типично для поршневых двигателей и, как это видно из сделанного анализа, заключается в непостоянстве крутящего момента. При этом, чем больше из­менения момента, тем больших изменений частоты вращения вала следует ожидать.

Для оценки неравномерности вращения вала вводится по­нятие степени неравномерности, под которой понимается от­
ношение максимального приращения угловой скорости колен­чатого вала к его средней угловой скорости при установившемся режиме:

(7.16)

где со_тС1Х и co_min - максимальное и минимальное значения угловой скорости, а со_ср = я п / 30 - средняя угловая скорость.

Из определения степени неравномерности следует, что рав­номерность вращения вала тем больше, чем меньше 8. Реко­мендуемые значения 8 лежат в пределах для двигателей:

главных, приводящих в движение гребной винт, 8 - 1/20-1/40; вспомогательных, приводящих в движение генераторы: постоянного тока 8 = 1/100 - 150, переменного тока 8 = 1/150- 1/300.

Вал двигателя, имеющего большее число цилиндров, враща­ется равномернее. Неравномерность вращения вала увеличивает­ся при выключении из работы одного или нескольких цилинд­ров, при увеличении неравномерности распределения мощности между цилиндрами и отклонений в значениях максимального давления цикла в цилиндрах. Для сохранения требуемой равно­мерности вращения вала необходимо, чтобы отклонения Р_{ и P_z в отдельных цилиндрах были минимальны и не превышали со­ответственно ±2,5 и ±5 % от их среднего значения для всех ци­линдров.

С увеличением махового момента вращающихся масс (а это равносильно увеличению запаса кинетической энергии) степень неравномерности 8 уменьшается. Поэтому для обеспечения более равномерного вращения вала маховой момент необходимо уве­личить; обычно для этого увеличивают маховой момент махо­вика G _м D², где G_M масса маховика, D его диаметр.

В судовых малооборотных двигателях в связи с большими вращающимися массами достаточно низкая степень неравно­мерности вращения обеспечивается самими вращающимися мас­сами, поэтому необходимость в маховике отпадает, а имею­щийся маховик в основном выполняет функцию колеса вало- поворотного механизма. При анализе причин, вызывающих неравномерное вращение вала, колебания угловой скорости,
вызываемые неравномерностью регулятора частоты вращения и волнением моря, не учитывались, так как эти колебания по частоте несоизмеримы с рассмотренными, их период во много раз превышает время одного оборота вала.

§ 7.3. Внешняя неуравновешенность и методы уравновешивания двигателей

Причины неуравновешенности. Понятие неуравновешенно­сти поршневых двигателей связывается с действием в них цикли­чески меняющихся сил и их моментов, вызывающих вибрацию, как самого двигателя, так и его фундамента и корпуса судна. К числу циклически меняющихся сил двигателя относятся силы действия газов в цилиндрах Рг и силы инерции движущихся масс Pj. Силы Р_г9 будучи направленными вверх и вниз, в преде­лах каждого цилиндра взаимно уравновешиваются (рис. 7.6, а), за пределы остова двигателя не передаются и поэтому не могут служить причиной его неуравновешенности.

Единственными силами, которые вызывают неуравнове­шенность и обусловленные ею вибрации, являются силы инерции и создаваемые ими моменты.

Силы инерции. Подразделяют эти силы на силы инерции поступательно движущихся масс, к которым относится поршень, шток и часть шатуна, и центробежные силы, создаваемые вра­щающимися массами. Силы инерции в одноцилиндровом двига­теле являются свободными и могут быть причиной вибрации.

Сила инерции поступательно движущихся масс описывает­ся формулой (7.6). Ввиду сложности закона ее изменения она может быть условно разделена на две составляющие:

Pj = Pji + PjjjTjxg:

Pj j ⁼ m_nR со² cos a = Pjcos a, (7.17) подчиняющаяся закону косинуса угла поворота кривошипа, называется силой инерции первого порядка;

Pj и ~ m_nRco k cos2a = PuCOs2a, (7.18)

подчиняющаяся закону косинуса удвоенного угла поворота кривошипа 2а, называется силой инерции второго порядка.

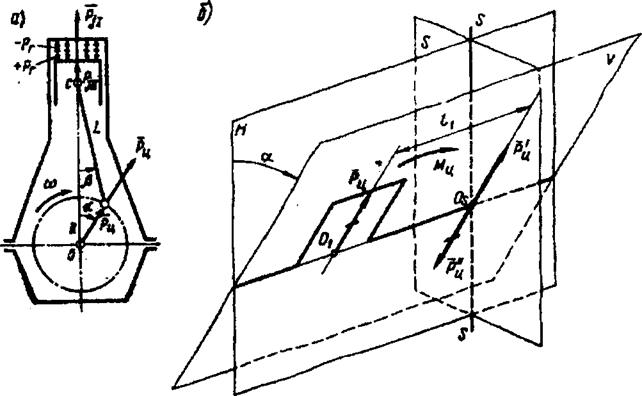Рис. 7.6. Силы инерции и моменты центробежных сил

Рис. 7.7. Характер изменения сил инерции первого и второго порядков

Силы Рл и Pju действуют в направлении движения по­ступательно движущихся масс - вдоль оси цилиндра, причем сила Pju в 2-5 раз меньше силы Рл, так как входящее в ее выражение X = 1/2,2 - 1/5. Обе силы приложены к центру го­ловного соединения (точка С на рис. 7.6, а) и при вращении кри­вошипа непрерывно меняют свои значения и знак, но при всех углах поворота кривошипа остаются в плоскости оси цилиндра (рис. 7.7).

Внешнее воздействие сил инерции I и II по­рядков - они стремятся оторвать двигатель от фундамента, ко­гда направлены вверх, и прижать к фундаменту, когда направле­ны вниз. Частота действия сил и вызываемых ими колебаний бу­дет кратна соответственно (сои 2 со, где со - угловая скорость).

Центробежная сила инерции, создающаяся при вращении

коленчатого вала, Рц = m_BpRco .

Эта сила постоянна по значению и направлена по радиусу кривошипа от центра кривошипного соединения к периферии. Масса вращающихся частей, как и поступательно движущихся, отнесенная к площади поршня, кг/м²,

Мщ SP + Мм + Мщ

Мвр ⁼-----------------------------

Fn

где Мщвр— масса вращающейся части шатуна, кг;

М_м = G_M /g ~ масса кривошипной шейки, кг; М_ш - неурав­новешенная масса двух щек, ориентировочно равная половине их массы, кг.

Центробежная сила инерции приложена к центру криво­шипного соединения (см. рис.7.6, а). Перенесем ее по линии действия в центр О коленчатого вала и в масштабе чертежа пред­ставим в виде радиуса-вектора Р_ц. При вращении вала вектор

Р_ц, лежащий в плоскости кривошипа, будет также вращаться, каждый раз занимая новое положение, соответствующее углу а, отсчитываемому от ВМТ. Иначе говоря, центробежная сила вращается вместе с валом, непрерывно меняя направление сво­его действия.

Внешнее воздействие центробежной силы инерции - в зависимости от положения кривошипа она стремит­ся сместить двигатель с фундамента в плоскостях, совпадающих в каждый момент с плоскостью кривошипа и проходящих через ось коленчатого вала.

Моменты сил инерции. Природу возникновения и действия моментов сил инерции разберем на примере центробежной силы одноцилиндрового двигателя, пространственная схема коленча­того вала которого приведена на рис. 7.6, б.

Допустим, что в рассматриваемый момент времени криво­шип отклонился от ВМТ на угол а и находится в плоскости V. Тогда возникающая в нем центробежная сила инерции Рц также лежит в этой плоскости и, будучи приложенной в точке Оj находится на расстоянии // от плоскости S, проходящей через центр тяжести двигателя.

Известно, что всякую силу Р, не нарушая ее действия, мож­но перенести параллельно самой себе в любую точку О, присое­динив при этом пару с моментом, равным моменту силы Р отно­сительно точки О]. Воспользовавшись этим правилом, приведем силу Р_и к центру 0₅ (Рис 7.6-6), являющемуся точкой пересече­ния оси вала с плоскостью центра тяжести S.

После приведения имеем: силу Рц, приложенную к центру О и стремящуюся оторвать двигатель от фундамента в плоскости V; пару сил Рц и Р"_ц, создающую на плече 11 момент Мц, дейст­вующий в той же плоскости V и стремящийся опрокинуть двига­тель относительно его центра тяжести в направлении по часовой стрелке.

Полученный момент Мц = Pj j lj = т _uRco~ (7.20) называется моментом центробежной силы; значение и направле­ние его определяются как самой силой, так и положением плос­кости центра тяжести двигателя относительно оси цилиндра.

Момент центробежной силы Мц как и сама сила Рц при вра­щении вала остаются неизменными и каждый раз, действуя в плос­кости колена, вращаются вместе с ним с угловой скоростью со.

Аналогично могут быть получены моменты сил инерции первого порядка Mj = Pjih = mnRco²cosa lj (7.21)

и второго порядка Мц = Pj uh~ m_nRco² Я cos 2 а //. (7.22) Поскольку силы Pji и Pjn действуют в вертикальной плос­кости (плоскости движения поршня), то и вызываемые ими мо­менты М\ и Мц действуют лишь в этой плоскости вне зависимо­сти от положения кривошипа.

Внешнее воздействие м о м е н т о в: центробежных сил - опрокинуть двигатель относительно его центра тяжести в плоскостях, проходящих через плоскость кривошипа и вращающихся вместе с ним;

сил инерции I и II порядков - опрокинуть двигатель относи­тельно его центра тяжести в вертикальной плоскости, проходя­щей через оси цилиндров.

Внешняя и внутренняя неуравновешенность многоци­линдрового дизеля. В пределах одного цилиндра возникают и действуют: центробежная сила инерции вращающихся масс Рц, сила инерции поступательно движущихся масс первого по­рядка Pju сила инерции поступательно движущихся масс вто­рого порядка Рщ, момент центробежной силы М_Ц9 моменты сил первого и второго порядков Mj и Мц.

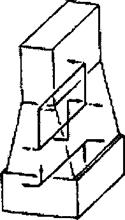
1. Момент первого породка в верт.пл.

2. Момент второго породка в верт.пл.

1. момент перв. порядка в гориз.пл.

Момент, прилож. к параллелям, от норм, силы, вертикальный

Момент, прилож. к параллелям, от ^ норм, силы, горизонтальный

А-давление сгорания В-нормальная сила С- сила затяга анкерных связей

D- сила на рамовые подшипники

Рис. 7.8. Силы и моменты, действующие в 2-х тактном двигателе

Силы и моменты в многоцилиндровом двигателе возникают и действуют в каждом цилиндре, и их суммарный эффект для двигателя в целом может быть получен путем нахождения сле­дующих векторных сумм:

2 2 Р}\\ 2 Р}ц\ 2 М_ц;

1 1

Если результаты суммирования оказываются равными ну­лю, то это свидетельствует о полной внешней уравновешенности двигателя.

Внешняя неуравновешенность двигателей

Результирующие силы инерции и моменты сил инерции

	И				25»		к я Н

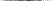
Нулевые значения векторных сумм могут быть получены, если одноименные силы, действующие во всех цилиндрах, и мо­менты сил, замыкаясь внутри остова двигателя, компенсиру­ют друг друга. Это означает, что внешнее воздействие резуль­тирующих векторов сил и моментов в данном случае отсутству­ет, т. е. на фундамент и корпус судна они не передаются.

Если же векторы сил или моментов при сложении компен­сируются лишь частично или совсем не компенсируются, то ре­зультирующие их векторы (суммы) будут выходить за пределы остова двигателя и оказывать внешнее воздействие в виде пере­менной периодически меняющейся нагрузки на фундамент и конструкции корпуса судна. В этом случае двигатель считается внешне неуравновешенным. Поскольку геометрическая сумма векторов зависит от их количества, размеров и взаимного распо­ложения, то внешняя неуравновешенность многоцилиндрового двигателя в общем случае определяется числом цилиндров и взаимным расположением кривошипов (углом заклинивания и порядком работы цилиндров). О характере внешней неуравно­вешенности двигателей с наиболее типичным расположением кривошипов можно судить по данным табл. 7.1.

Помимо внешнего воздействия сил инерции и их момен­тов, последние, действуя внутри остова двигателя, нагружают и деформируют его конструкции. Центробежные силы, действуя в плоскости колена вала, а силы инерции I и II порядков - в плос­кости осей цилиндров, нагружают коленчатый вал и подшипни­ки и передаются фундаментной раме. Одновременно вал нагру­жается моментами Мц, Mi и Мц, которые стремятся изогнуть вал в плоскостях их действия; деформация вала воспринимается подшипниками (особенно центральными, испытывающими наи­большую нагрузку) и фундаментной рамой, в которой они рас­положены. В итоге в фундаментной раме, как и на валу, под действием моментов сил инерции возникают напряжения изгиба и деформации. Отмеченное действие сил инерции внутри остова двигателя определяет внутреннюю неуравновешенность двигателя.

Заметим, что независимо от степени и характера внешней неуравновешенности двигателя внутренне он всегда остается неуравновешенным.

Из формул (7.17)-(7Л9) видно, что чем больше частота вращения вала и больше масса движущихся частей, тем больше силы инерции и больше сказывается их воздействие на остов самого двигателя (внутренняя неуравновешенность) и его фун­дамент (внешняя неуравновешенность).

Методы уравновешивания. Внешняя неуравновешен­ность двигателя, особенно если неуравновешенные силы и мо­менты значительны, может вызывать последствия, связанные с вибрацией как самого двигателя, так и соединенных с ним кон­струкций корпуса судна. Поэтому в отдельных случаях для уменьшения вибрации прибегают к уравновешиванию возни­кающих в двигателе сил и моментов.

Уравновешивание центробежных сил осуществляется пу­тем установки на щеках кривошипов противовесов (рис.7.9). При вращении в кривошипе одного цилиндра возникает центро­бежная сила Рц, лежащая в плоскости кривошипа, Рц = m_BpRco², где т_Вр - масса неуравновешенной части кривошипа (криво­шипная шейка и часть массы щек) и ориентировочно равна 0,6 массы шатуна, участвующей во вращательном движении, кг; R - радиус кривошипа, м.

Сила Р_ц может быть уравновешена двумя противовесами, укрепленными на щеках кривошипа. Они развивают центро­

бежную силу 2Р_пр ~ Рц. Тогда можно записать т_Вр = 2mnpRco - 2 тпррсо² или при равенстве угловых скоростей масс двигателя и противовесов т_ВР Rco² = 2т_ПРр, где т_пр - масса одного противо­веса, кг; р - радиус инерции проти­вовеса, равный расстоянию от его центра тяжести до оси вращения, м.

При наличии в системе неуравнове­шенного момента имеются две возмож­ности его погасить: первая приводит к уравновешиванию центробежных сил

в пределах каждого цилиндра, вторая - к уравновешиванию сво­бодного момента системы парой противовесов, развивающих рав­ный, но противоположный по знаку момент. Расстояние между этими противовесами желательно выбирать максимально боль­шим, с тем, чтобы по возможности уменьшить их массу.

Иногда прибегают к установке про­тивовеса для разгрузки рамовых подшипников. В этом случае проти­вовесы часто навешивают на щеки под углом к их оси. Уравновешивание сил инерции I и II порядков, возни­кающих от поступательно движу­щихся масс цилиндра, невозможно осуществить с помощью противове­сов, установленных на щеки вала, так как центробежная сила противо­весов, находясь в плоскости колена, при вращении вала непрерывно ме­няет плоскость своего действия. Не­обходимо же иметь уравновеши­вающую силу только в вертикальной плоскости. Задача может быть реше­на, если использовать две массы, вращающиеся в разные стороны (рис. 7.10). Эти массы заклинены на дополнительных валах таким образом, что создаваемые при их вращении вертикальные составляющие Рцв центробежных сил складываются и дают составляющую 2Рцв ⁼ Pj и но противоположно направленную, которая и урав­новешивает силу Pjj первого порядка. Горизонтальные состав­ляющие Рцг взаимно уничтожают друг друга. Таким образом можно уравновесить и силу инерции 2-го порядка, но для этого необходимо, чтобы противовесы вращались в противоположные стороны с удвоенной угловой скоростью 2со.

Изложенный метод известен под наименованием «Ланче- стер Балансир».

Уравновешивая силы, можно подобным образом уравнове­сить и создаваемые ими моменты М/ и Мц. Как видно из табли­цы 7.1, двухтактные двигатели имеют неуравновешенные мо­менты от сил первого и второго порядков, значения которых согласно формулам 7.21 и 7.22 пропорциональны радиусу кри­вошипа R и отношению L = Я . В современных длинноходовых двигателях величины R и L возросли примерно в 1,8 раза, что не

могло не отразиться на росте сил инерции и вызываемых ими моментов. Этим объясняется, что в крейцкопфных двигателях более ранних конструкций метод «Ланчестер Балансир» не находил применения, а использовался исключительно в высоко-

и среднеоборотных двига­телях, для которых харак­терно наличие больших сил инерции в силу высоких оборотов, то с появлением длинноходовых конструк­ций его стали применять и в них. Иллюстрацией служит рис. 7.11.

Рис. 7.11. Уравновешивания моментов в крейцкопфном двигателе

§ 7. 4. Продольные и крутильные колебания вала

Продольные колебания

Этот вид колебаний возникает под действием тангенциальной Т и радиальной Z составляющих сил действия газов и сил инер­ции масс, нагружающих кривошипы коленчатого вала и вызы­вающих деформацию колен в виде попеременного расхождения или сближения щек (рис. 7.12). В итоге вал приобретает колеба­ния вдоль оси, которые передаются упорному подшипнику, а че­рез него фундаменту и корпусу судна. Продольные колебания ста­ли особенно заметными с ростом форсирования двигателей, так как увеличилось отношение p_z/р_е с 7,5 до 10. Продольные коле­бания возбуждаются также меняющимся упором гребного винта из-за пульсирующего характера действия воды на вращающиеся лопасти и крутильных колебаний валопровода и винта. В целях уменьшения продольных колебаний коленчатого вала и вызывае­мых ими вибраций судна на носовой фланец вала устанавливают
гидравлический демпфер поршневого типа (см. рис. 7.17).

Рис. 7.12. Схема деформациии кривошипа при продольных колебаниях

Колебания в поперечной плоскости

Малооборотаый крейцкопфный двигатель, имеющий боль­шую высоту, раскачивается в поперечной плоскости под дейст­вием моментов, возникающих в пределах каждого цилиндра от нормальных сил N, передаваемых через крейцкопфный узел па­раллелям. Частота этих колебаний невелика и равна произведе­нию п i (где / - число цилиндров). Для самого двигателя эти ко­лебания неопасны, но они могут вызвать нежелательные высокие местные напряжения в наборе второго дна корпуса судна под фундаментом двигателя.

Чтобы этого избежать, остов двигателя в его верхней части раскрепляется с набором корпуса судна в зоне главной палубы с помощью двух пар поперечных связей / (рис. 7.13), снабженных эластичным гидравлическим звеном 2. Наличие этого звена позволяет сохранять постоянной силу натяже­ния связей вне зависимости от возможных при изменении загрузки судна (плавание в балласте или в грузу) деформаций его корпуса.

Крутильные колебания

В дизельной установке крутильные колебания испытывают коленчатый вал, промежуточные и гребной валы с навешенными на них массами (детали механизма движения отдельных цилинд-

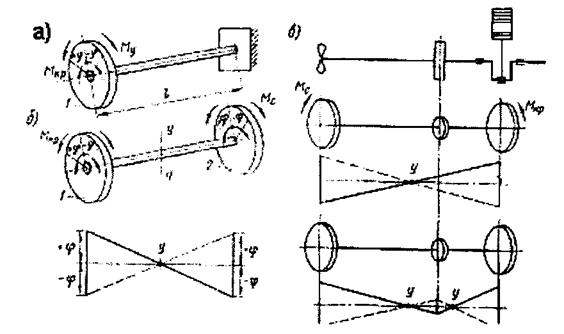Рис. 7.14. Одно-, двух- и трехмассовые крутильные системы

ров, маховик, соединительные муфты, гребной винт), связанные в единую упругую систему валопровода.

Крутильные колебания представляют собой периодические колебания в плоскости вращения навешенных на вал масс, при которых участки вала между массами скручиваются и раскручи­ваются под действием циклически меняющегося крутящего мо­мента.

Любая конструкция под действием переменных сил испы­тывает два вида колебаний - свободные и вынужденные.