Теоремы сложения и умножения вероятностей. Пусть - два случайных события.

Теорема сложения

Пусть 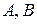- два случайных события.

Теорема сложения.Вероятность суммы двух событий или вероятность появления хотя бы одного из них равна сумме вероятностей этих событий минус вероятность их совместного появления:

.

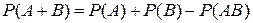Для несовместных событий 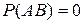, поэтому теорема примет вид:

.

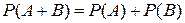Для произвольного числа слагаемых:

;

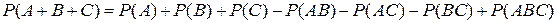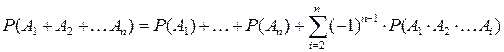
Следствие.

1. Очевидно, что 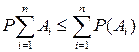- вероятность суммы событий не превышает сумму вероятностей этих событий.

2. 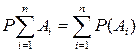, если события попарно несовместны.

3. Если события образуют полную группу, то есть 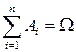, то .

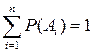Условная вероятность

Пусть 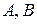- совместные события.

Условной вероятностью события 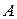при условии, что событие 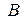произошло, называется число, определяемое равенством
.
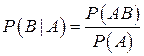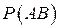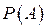Здесь и - вероятности, причём .

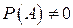События 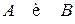называются зависимыми, то есть вероятность события 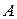зависит от того, произошло или нет событие .

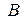Теорема умножения

Теорема умножения. Вероятность произведения двух событий равна произведению вероятностей одного из них, умноженной на условную вероятность другого при условии, что первое событие произошло.

.

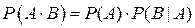Для трех слагаемых ;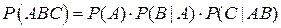

для последовательности 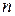событий

.

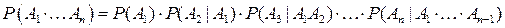В последней формуле вероятность произведения 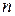событий равна произведению вероятности одного из них на условные вероятности всех остальных событий, причем вероятность каждого последующего вычисляется в предположении, что все предыдущие уже произошли.