Классическое определение вероятности. Из этой первой лекции по теории вероятностей я запомнил только полузнакомый термин «математическое ожидание»
... Из этой первой лекции по теории вероятностей я запомнил только полузнакомый термин «математическое ожидание». Незнакомец употреблял этот термин неоднократно, и каждый раз я представлял себе большое помещение, вроде зала ожидания, с кафельным полом, где сидят люди с портфелями и бюварами и, подбрасывая время от времени к потолку монетки и бутерброды, сосредоточенно чего-то ожидают. До сих пор я часто вижу это во сне. Но тут незнакомец оглушил меня звонким термином «предельная теорема Муавра — Лапласа» и сказал, что все это к делу не относится.
Аркадий и Борис Стругацкие, Стажеры.
Предположим, что мы имеем дело с дискретным пространством элементарных исходов, то есть пространством, состоящим из конечного или счетного числа элементов:
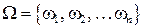 .
.
Поставим каждому элементарному исходу 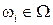 в соответствие число
в соответствие число 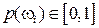 так, что
так, что 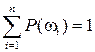 .
.
Назовем число 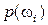 вероятностью элементарного исхода
вероятностью элементарного исхода 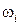 .
.
Вероятностью события 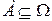 называется число
называется число 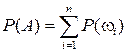 ,
,
равное сумме вероятностей элементарных исходов, входящих в событие 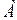 .
.
Множество элементарных событий образует полную группу событий, если в результате испытания появиться хотя бы одно из них.
События называются равновозможными, если ни одно из них не является более возможным, чем другое.
Например, при бросании игральной кости выпадение чисел 1,2, …6 – события равновозможные.
Предположим, что мы имеем дело с пространством элементарных исходов, состоящим из конечного числа N элементов, образующих полную группу событий: 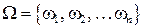 . Более того, будем считать все элементарные исходы равновозможными. Тогда вероятность любого из них принимается равной
. Более того, будем считать все элементарные исходы равновозможными. Тогда вероятность любого из них принимается равной 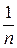 .
.
Если событие 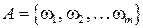 состоит из
состоит из 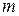 элементарных исходов (благоприятствующихпоявлениюсобытия
элементарных исходов (благоприятствующихпоявлениюсобытия 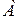 ), то вероятность этого события равняется
), то вероятность этого события равняется
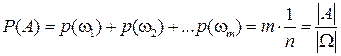 ,
,
где символом 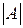 обозначено число элементарных исходов
обозначено число элементарных исходов 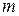 , в которых событие
, в которых событие 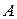 произошло.
произошло.
В этом случае вероятность любого события 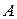 вычисляется по формуле
вычисляется по формуле
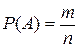 ,
,
называемой классическим определением вероятности. Эта формула читается так: «вероятность события 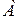 равна отношению числа исходов, благоприятствующих событию
равна отношению числа исходов, благоприятствующих событию 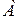 , к общему числу исходов».
, к общему числу исходов».
Свойства вероятности:
1. 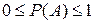 – вероятность любого события есть положительное число, заключенное от 0 до 1.
– вероятность любого события есть положительное число, заключенное от 0 до 1.
2. 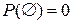 – вероятность невозможного события равна 0.
– вероятность невозможного события равна 0.
3. 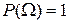 – вероятность достоверного события равна 1.
– вероятность достоверного события равна 1.
Пример. В урне 12 шаров: 3 белых, 4 черных, 5 красных. Какова вероятность вынуть из урны черный шар?
Решение. Эксперимент состоит в случайном выборе из закрытой урны одного шара. Элементарным исходом опыта является номер шара и его цвет. Поскольку все исходы равновероятны, можно использовать классическое определение вероятности. Общее число элементарных исходов 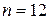 (количество шаров в урне). Событию
(количество шаров в урне). Событию 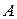 ={извлекли черный шар}благоприятствуют
={извлекли черный шар}благоприятствуют 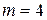 исходов (количество черных шаров). Получаем, что
исходов (количество черных шаров). Получаем, что
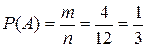 .
.
Дата добавления: 2016-04-22; просмотров: 1194;
