Свободные колебания
1. Колебания. Общий подход к изучению колебаний различной физичес
кой природы.
Колебаниями называются движения или процессы, которые обладают определенной повторяемостью во времени.
Колебания сопровождаются попеременным превращением энергии одного вида в энергию другого вида.
Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии, без дальнейшего внешнего воздействия на колебательную систему (систему, совершающую колебания). Колебания называются вынужденными, если они происходят под действием периодически изменяющейся внешней силы.
Физическая природа колебаний может быть разной — различают механические, электромагнитные и др. колебания.
Но различные колебательные процессы описываются одинаковыми уравнениями, поэтому целесообразно изучать все колебательные процессы, используя общие свойства колебаний.
2. Гармонические колебания и их характеристики.
Гармоническими колебаниями называются колебания, при которых колеблющаяся физическая величина изменяется по закону синуса (или косинуса).
Различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) могут быть представлены в виде суммы (суперпозиции) гармонических колебаний.
Гармоническое колебание величины s описывается уравнением типа
s = A·cos(ωt +φ)
где:
А -амплитуда колебания — максимальное значение колеблющейся величины;
ω- круговая (циклическая) частота;
φ - начальная фаза колебания в момент времени t=0;
(ωt +φ)- Фаза колебания в момент времени t.
Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до -1, то s может принимать значения от + А до - А .
Поскольку cos(a + 2π) = cosa, то при гармонических колебаниях увеличение (приращение) фазы колебания на 2π приводит к тому, что все величины, характеризующие колебание, принимают исходное значение.
Периодом колебанийT называется наименьший промежуток времени, по истечении которого повторяются состояния колеблющейся системы (совершается одно полное колебание) и фаза колебания получает приращение 2π
ω(t + T) + φ = (ωt + φ ) + 2 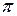
Откуда
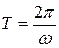
Частотой колебанийn называется величина обратная периоду колебаний — число полных колебаний, совершаемых в единицу времени
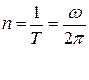
Единица частоты — герц (Гц)— частота периодического процесса, при котором за 1 секунду совершается один цикл колебаний.
3. Дифференциальное уравнение гармонических колебаний.
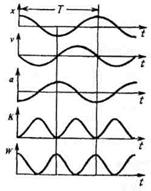
Первая (скорость) и вторая (ускорение) производные по времени от гармонически колеблющейся величины s также совершают гармонические колебания с той же циклической частотой:
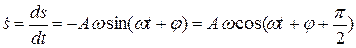
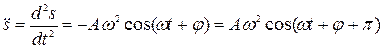
Из последнего уравнения видно, что s удовлетворяет уравнению
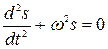 или
или 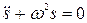
Это уравнение называется дифференциальным уравнением гармонических колебаний. Его решение:
s = A·cos(ωt + φ).
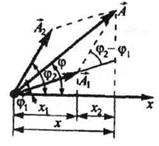
4. Метод векторных диаграмм.
|
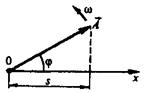
Из произвольной точки О, выбранной на оси х, под углом φ, равным начальной фазе
колебания, откладывается вектор А, модуль которого равен амплитуде А, рассматриваемого колебания. Если этот вектор будет вращаться
вокруг точки О с угловой скоростью со, то проекция вектора на ось х будет совершать колебания по закону s = A·cos(ωt + φ).
5. Экспоненциальная форма записи гармонических колебаний.
Согласно формуле Эйлера для комплексных чисел
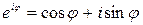
где 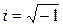 — мнимая единица. Поэтому уравнение гармонического колебания s = A·cos(ωt +φ) можно записать в комплексной экспоненциальной форме:
— мнимая единица. Поэтому уравнение гармонического колебания s = A·cos(ωt +φ) можно записать в комплексной экспоненциальной форме:
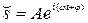
Физический смысл имеет только вещественная часть комплексной функции 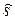 , которая и представляет собой гармоническое колебание:
, которая и представляет собой гармоническое колебание:
Re( 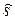 ) = A cos(ωt +φ) = s
) = A cos(ωt +φ) = s
6. Механические гармонические колебания.
Пусть материальная точка совершает прямолинейные гармонические
|
Смещение: х= A·cos(ωt + φ)
Скорость: 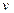 =
= 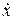 = -Аωcos(ωt + φ +
= -Аωcos(ωt + φ + 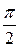 )
)
Ускорение:
a = 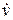 =
= 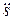 =Аω2 cos(ωt + φ +
=Аω2 cos(ωt + φ + 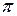 )
)
Амплитуды скорости и ускорения равны Aω и Aω2
Фаза скорости отличается от фазы смещения на 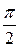 , а фаза ускорения на
, а фаза ускорения на 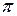 .
.
Сила, действующая на колеблющуюся материальную точку массой т равна
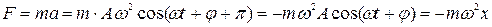
Таким образом, сила пропорциональна смещению материальной точки и
направлена в сторону, противоположную смещению (к положению равновесия).
Такая зависимость от смещения характерна для упругих сил и поэтому силы,
которые аналогичным образом зависят от смещения, называются
Квазиупругими.
7. Энергия материальной точки, совершающей гармонические колебания.
Кинетическая энергия материальной точки:
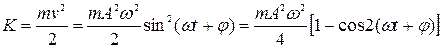
Потенциальная энергия материальной точки, совершающей гармонические колебания под действием квазиупругой силы:
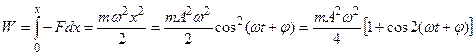
Полная энергия: 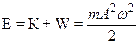
остается постоянной, с течением времени происходит только превращение кинетической энергии в потенциальную и обратно.
8. Гармонический осциллятор.
Гармоническим осциллятором называется система, совершающая колебания, описываемые дифференциальным уравнением
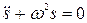
Примерами гармонического осциллятора являются пружинный, математический и физический маятники и электрический колебательный контур.
9. Пружинный маятник.
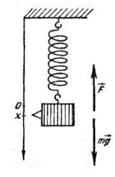
Пружинный маятник — это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы
|
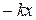
где 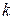 — жесткость пружины.
— жесткость пружины.
Уравнение движения маятника
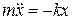 или
или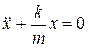
Сравнивая это уравнение с уравнением движения
гармонического осциллятора 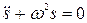 , мы видим, что пружинный маятник совершает колебания по закону
, мы видим, что пружинный маятник совершает колебания по закону 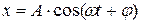 с циклической частотой и периодом:
с циклической частотой и периодом:
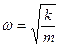

Потенциальная энергия пружинного маятника:
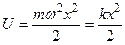
Если на маятник действует сила трения, пропорциональная скорости 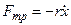 ,где r — коэффициент сопротивления, то колебания маятника будут
,где r — коэффициент сопротивления, то колебания маятника будут
затухающими и закон движения маятника будет иметь вид  или
или
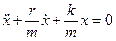
10. Математический маятник.
Математическим маятникомназывается идеализированная система,
|
Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой цлинной нити.
При малых углах отклонения а можно считать: x≈lα.
Возвращающая сила:
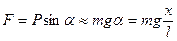
Уравнение движения:
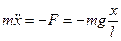 или
или 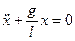
Следовательно, движение математического маятника описывается дифференциальным уравнением гармонических колебаний, то есть происходит по закону х= A·cos(ωt + φ) с частотой и периодом, соответственно:
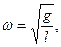
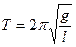
11 .Физический маятник.
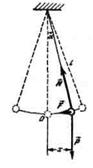
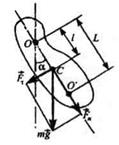
Физическим маятником называется твердое тело, совершающее под действием силы тяжести колебания вокруг горизонтальной оси подвеса, не проходящей через центр масс тела.
|
Если физический маятник отклонен из положения равновесия на некоторый угол а, то момент возвращающей силы
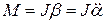
С другой стороны, при малых углах
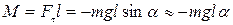
где J — момент инерции маятника относительно оси, проходящей через точку подвеса О,
l - расстояние между точкой подвеса и центром масс С маятника,
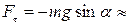 — возвращающая сила (со знаком минус, поскольку она всегда направленная противоположно направлению увеличения a).
— возвращающая сила (со знаком минус, поскольку она всегда направленная противоположно направлению увеличения a).
Следовательно: 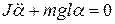 , или
, или
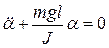
Таким образом, при малых колебаниях физический маятник совершает гармонические колебания  с циклической частотой и периодом:
с циклической частотой и периодом:
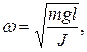
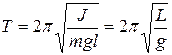
где длина 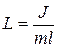 — называется приведенной длиной физического ml маятника.
— называется приведенной длиной физического ml маятника.
Приведенная длина физического маятника — это длина такого математического маятника, который имеет такой же период колебаний, что и данный физический маятник.
Точка О' на продолжении прямой ОС, отстоящая от оси подвеса на расстоянии приведенной длины L, называется центром качаний физического маятника.
Математический маятник можно представить как частный (предельный) случай физического маятника, вся масса которого сосредоточена в его центре
масс. При этом J = ml2, следовательно 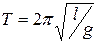 .
.
12.Сложение гармонических колебаний.
Если система одновременно участвует в нескольких колебательных процессах, то под сложением колебаний понимают нахождение закона,
|
процесс.
Для сложения колебаний х1 и х2 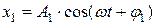 ,
, 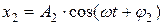 используем метод вращающегося вектора амплитуды (метод векторных диаграмм).
используем метод вращающегося вектора амплитуды (метод векторных диаграмм).
Так как векторы А1, и А2 вращаются с одинаковой угловой скоростью ω, то разность фаз 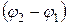 между ними остается постоянной. Уравнение результирующего колебания будет
между ними остается постоянной. Уравнение результирующего колебания будет
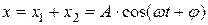
где амплитуда А и начальная фаза φ задаются соотношениями:
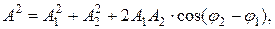
где
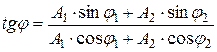
Сумма двух гармонических колебаний одного направления и одинаковой частоты есть гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания.
Амплитуда результирующего колебания зависит от разности фаз складываемых колебаний:
1) 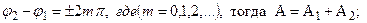
2) 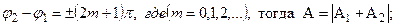
13. Биения.
Биениями называются периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами.
Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω <<ω. Путь для простоты начало отсчета выбрано так, чтобы начальные фазы обоих колебаний были равны нулю:

|
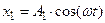 ,
, 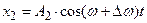
Результирующее колебание будет иметь вид:
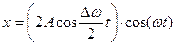
— гармоническое колебание с частотой ω, амплитуда которого изменяется по
закону 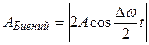 с частотой
с частотой 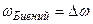 (частота биений вдвое больше частоты изменения косинуса, поскольку
(частота биений вдвое больше частоты изменения косинуса, поскольку 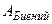 берется по модулю).
берется по модулю).
14. Разложение Фурье.
Любое сложное периодическое колебание S=f(t) можно представить в виде суммы простых гармонических колебаний с циклическими частотами, кратными основной циклической частоте ω 0:
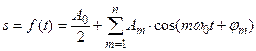
Такое представление периодической функции f(t) называется разложением ее в ряд Фурье или гармоническим анализом сложного периодического колебания.
Члены ряда Фурье, соответствующие гармоническим колебаниям с циклическими частотами ω0, 2ω0, 3ω0 и т. д., называются первой (или основной), второй, третьей и т. д., гармониками сложного периодического колебания S=f(t).
Совокупность этих гармоник образует спектр колебания S=f(t).
15. Сложение взаимно перпендикулярных гармонических колебаний одинаковой частоты.
Пусть два гармонических колебания одинаковой частоты ω, происходят во взаимно перпендикулярных направлениях вдоль осей х и у. Для простоты выберем начало отсчета так, чтобы начальная фаза первого колебания была равна нулю:
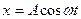 ,
, 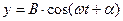
где α- разность фаз колебаний, а А и В — их амплитуды. Уравнение траектории результирующего колебания (исключая t из уравнений) есть уравнение эллипса, произвольно расположенного относительно координатных осей:
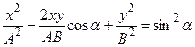
и такие колебания называются эллиптически поляризованными.
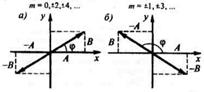
16.Линейно поляризованные колебания.
|
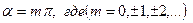 , тоэллипс вырождается в отрезок прямой
, тоэллипс вырождается в отрезок прямой
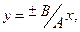
где знак плюс соответствует нулю и четным значениям т, а знак минус — нечетным значениям т.
Результирующее колебание является гармоническим колебанием с
частотой ω и амплитудой 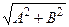 и совершается вдоль прямой,
и совершается вдоль прямой,
составляющей с осью х угол 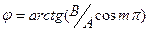 . Такие колебания
. Такие колебания
называются линейно поляризованными колебаниями.
17. Циркулярно поляризованные колебания.
Если разность фаз 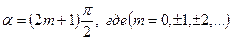 , то в данном случае
, то в данном случае
|
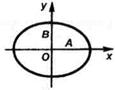
уравнение траектории принимает вид:
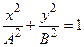
Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам А и В.
ЕслиА=В, то эллипс вырождается в окружность, и такие колебания называются циркулярно поляризованными или колебаниями, поляризованными по кругу.
18 .Фигуры Лиссажу.
Если взаимно перпендикулярные колебания происходят с циклическими частотам р ω и q ω, где q и р — целые числа:
 ,
, 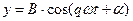
то значения координат х и у одновременно повторяются через одинаковые промежутки времени Т0 равные наименьшему общему кратному периодов 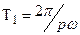 и
и 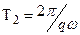 колебаний вдоль осей х и у. Траектории замкнутых
колебаний вдоль осей х и у. Траектории замкнутых
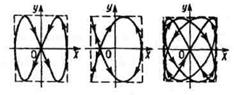
|
кривых, которые получаются в этих случаях, называются фигурами Лиссажу. Вид этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. На рисунке показан вид фигур Лиссажу при трех различных
значениях отношения (2:1, 3:2, 4:3) и разности фаз 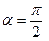 .
.
Дата добавления: 2016-04-22; просмотров: 2432;