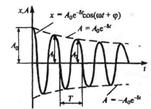
Дифференциальное уравнение свободных затухающих колебаний
линейной системы имеет вид
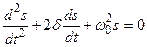
где s- колеблющаяся величина,
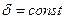— коэффициент затухания,
ω0- циклическая частота свободных незатухающих колебаний той же колебательной системы (при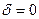 
).
|
) решение этого уравнения:
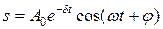
где:
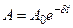— амплитуда затухающих колебаний,
А0- начальная амплитуда,
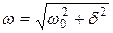— циклическая частота затухающих колебаний.
Промежуток времени 
, в течение которого амплитуда затухающих о
колебаний уменьшается в е раз называется временем релаксации.
Затухание нарушает периодичность колебаний.
Затухающие колебания не являются периодическими.
Однако если затухание мало, то можно условно пользоваться понятием периода затухающих колебаний как промежутка времени между двумя последующими максимумами колеблющейся физической величины:
21. Декремент затухания.
Если A(t) и A(t + T) — амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающихся на период, то отношение
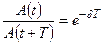
называется декрементом затухания, а его логарифм
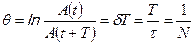
называется логарифмическим декрементом затухания.
Здесь N — число колебаний, совершаемых за время уменьшения амплитуды в ераз.
22.Добротность колебательной системы.
Добротностью колебательной системы называется безразмерная величина Q, равная произведению 2π на отношение энергии W(t) колебаний системы в произвольный момент времени t к убыли этой энергии за промежуток времени от t до t + T (за один условный период затухающих колебаний):
Энергия W(t) пропорциональна квадрату амплитуды А(t), поэтому:
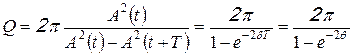
При малых значениях логарифмического декремента затухания (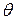 
<<1)
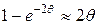, поэтому (принимая Т ≈Т0)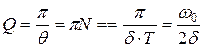 
Дата добавления: 2016-04-22; просмотров: 891;