Элементы специальной теории относительности
37. Преобразования Галилея
В классической механике, при скоростях тел значительно меньших, чем скорость света (υ<<c), справедлив механический принцип относительности (принцип относительности Галилея): законы динамики одинаковы во всех инерциальных системах отсчета.
Рассмотрим две системы отсчета: инерциальную систему К (с координатами x,y,z), которую будем считать неподвижной, и систему 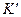 (с координатами x',y',z'), движущуюся относительно К равномерно и прямолинейно с постоянной скоростью
(с координатами x',y',z'), движущуюся относительно К равномерно и прямолинейно с постоянной скоростью 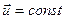
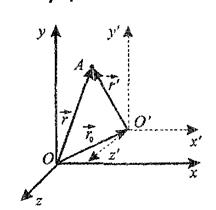
В начальный момент времени начала координат O и 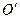 этих систем совпадают.
этих систем совпадают.
В произвольный момент времени t: 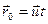
Для произвольной точки А: 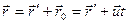 . Или в проекциях на оси координат:
. Или в проекциях на оси координат:
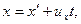
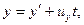
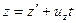
Эти соотношения называются преобразованиями координат Галилея.
Продифференцировав их по времени, получимправило сложения скоростей в классической механике:
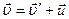
В классической механике предполагается, что ход времени не зависит от
относительного движения систем отсчета, поэтому к преобразованиям Галилея
можно добавить еще одно соотношение: t = t'
Ускорение в системах отсчета, движущихся относительно друг друга равномерно и прямолинейно, одинаково: 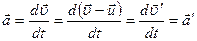 . Это и служит доказательством принципа относительности Галилея.
. Это и служит доказательством принципа относительности Галилея.
38.Постулаты Эйнштейна.
1)Принцип относительности: никакие опыты, проведенные внутри данной инерциальной системы отсчета, не дают возможность обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной системы отсчета к другой.
2)Принцип инвариантности скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.
39.Преобразования Лоренца.
Пусть система О' движется относительно системы О со скоростью υ = const, причем 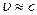 (с - скорость света (скорость распространения электромагнитных взаимодействий) в вакууме). Обозначим отношение скоростей υ и с через
(с - скорость света (скорость распространения электромагнитных взаимодействий) в вакууме). Обозначим отношение скоростей υ и с через 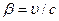 . Пусть вектор скорости
. Пусть вектор скорости 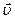 направлен вдоль оси ОХ. Тогда релятивистские преобразования координат и времени будут иметь вид:
направлен вдоль оси ОХ. Тогда релятивистские преобразования координат и времени будут иметь вид:
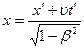 ,
, 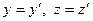 ,
, 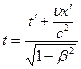
Эти соотношения — преобразования Лоренца υ<<c переходят в преобразования Галилея.
Они устанавливают взаимосвязь пространства и времени — в закон преобразования координат входит время, а в закон преобразования времени — пространственные координаты.
Следствием этого является тот факт, что если два события в системе О происходят одновременно но в разных точках ( 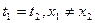 ), то в системе О' эти события, оставаясь пространственно разобщенными, оказываются и неодновременными.
), то в системе О' эти события, оставаясь пространственно разобщенными, оказываются и неодновременными.
Пусть в некоторой точке х в системе О происходит событие длительностью 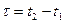 , то в системе О' длительность этого же события
, то в системе О' длительность этого же события
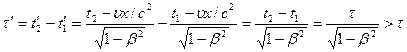
Т.о. длительность события, происходящего в некоторой точке, наименьшая в той инерциальиой системе отсчета, относительно которой эта точка неподвижна. Следовательно, часы, движущиеся относительно инерциальиой системы отсчета, идут медленнее покоящихся часов.
Рассмотрим стержень, расположенный вдоль оси 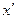 и покоящийся относительно системы О'. Его длина в системе О' будет
и покоящийся относительно системы О'. Его длина в системе О' будет 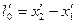 . Чтобы определить длину
. Чтобы определить длину 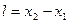 этого стержня в системе О, относительно которой он движется со скоростью υ, измерим координаты его концов х1 и х2 в один и тот де момент времени t.
этого стержня в системе О, относительно которой он движется со скоростью υ, измерим координаты его концов х1 и х2 в один и тот де момент времени t.
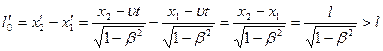
Размер тела, движущегося относительно инерциальиой системы отсчета, уменьшается в направлении движения, причем лоренцово сокращение длины тем больше, чем больше скорость движения. Поперечные размеры теп не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета.
Если материальная точка движется в системе О' вдоль оси х' со скоростью 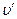 , а сама система О' движется со скоростью и относительно системы О, то релятивистский закон сложения скоростей:
, а сама система О' движется со скоростью и относительно системы О, то релятивистский закон сложения скоростей:
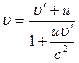
В качестве величины, инвариантной по отношению к преобразованию координат в четырехмерном пространстве Эйнштейна (не зависящей от выбора системы отсчета) вводится интервал между событиями:
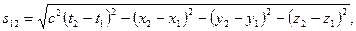 где
где 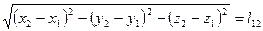 — расстояние между точками обычного трехмерного пространства. Обозначив
— расстояние между точками обычного трехмерного пространства. Обозначив 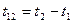 , получим
, получим
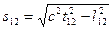
40. Основные соотношения релятивистской динамики.
Релятивистская масса m движущихся релятивистских частиц (тел) зависит от их скорости.
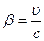
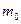 — масса покоя частицы, т.е. масса, измеренная в той инерциальиой системе отсчета, в которой частица находится в покое.
— масса покоя частицы, т.е. масса, измеренная в той инерциальиой системе отсчета, в которой частица находится в покое.
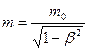
Релятивистский импульс 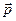 . Релятивистский импульс системы сохраняется. Закон сохранения релятивистского импульса — следствие однородности пространства.
. Релятивистский импульс системы сохраняется. Закон сохранения релятивистского импульса — следствие однородности пространства.
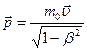
 Основной закон релятивистской динамики:
Основной закон релятивистской динамики:
Законы классической динамики получаются из законов релятивистской динамики в предельном случае υ<<c (или 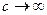 ). Т.о. классическая механика - это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме).
). Т.о. классическая механика - это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме).
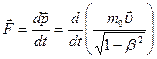
Полная энергия тела массы т:
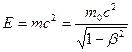
Соотношение 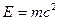 носит универсальный характер, оно применимо ко всем формам энергии, т.е. можно утверждать, что с энергией, какой бы формы она не была, связана масса
носит универсальный характер, оно применимо ко всем формам энергии, т.е. можно утверждать, что с энергией, какой бы формы она не была, связана масса 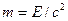 и, наоборот, со всякой массой связана энергия. Покоящееся тело обладает энергией:
и, наоборот, со всякой массой связана энергия. Покоящееся тело обладает энергией: 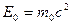 , называемой энергией покоя.
, называемой энергией покоя.
Полная энергия замкнутой системы сохраняется. Закон сохранения энергии — следствие однородности времени.
Кинетическая энергия: 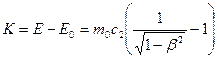
Релятивистское соотношение между полной энергией и импульсом тела:
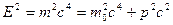
Величина 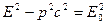 является инвариантом системы.
является инвариантом системы.
В случае, когда масса покоя частицы равна нулю, то 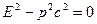 . Следовательно, такая частица может обладать отличными от нуля энергией и импульсом только в том случае, когда она движется со скоростью света. К таким частицам относятся фотоны.
. Следовательно, такая частица может обладать отличными от нуля энергией и импульсом только в том случае, когда она движется со скоростью света. К таким частицам относятся фотоны.
Основной вывод теории относительности — пространство и время органически взаимосвязаны и образуют единую форму существования материи — пространство-время.
Дата добавления: 2016-04-22; просмотров: 962;
