Дискретті канал бойынша кедергісіз беру үшін ақпаратты кодтау
Хабарларды беру немесе сақтау сандарды беру мен сақтауға апарады. Сандарды қандай да бір санау жүйесінде талдауға болады. Осылай берілген санау жүйесіне негізделген кодтардың біреуі алынады.
Позициялы санау жүйесі үшін сан келесі түрде анықталады:
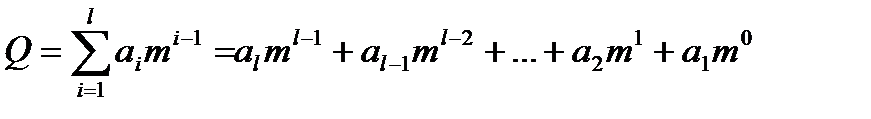
мұндағы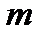 
– санау жүйесінің негізделуі, 
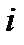– берілген сан разрядының номері, 
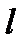– разрядтар саны; 
– 
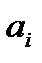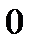мен 
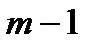шегіндегі кез келген бүтінсанды мәндерді қабылдайтын және санда 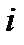-ші разрядты бірлік қанша бар екенін көрсететін көбейткіш.
Ең эффективті жүйе болып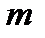 
әртүрлі символдар санының ең кіші туындысын үштік кез келген санын өрнектеу үшін разрядтар санында қамтамасыз ету (бұл минимум анықталған ондық үлкен 
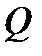санының жаңғыруы үшін 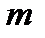және 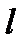арасында көрсетілген байланыс графигінде суреттелген.).
Екілік жүйенің артықшылығы: логикалық элементтер екі берік жағдайдан тұрады.
Арифметикалық и логикалық әрекеттер екілік жүйеде қарапайым түрде жүзеге асырылады:
| Қосу ережесі | Азайту ережесі | Көбейту ережесі |
| 0+0=0 | 0-0=0 | 0*0=0 |
| 0+1=1 | 1-0=1 | 0*1=0 |
| 1+0=1 | 1-1=0 | 1*0=0 |
| 1+1=10 | 10-1=1 | 1*1=1 |
Кодтауда және кодпен хабарлауда ең кең тараған логикалық операция – екінің модулі бойынша қосу. Екілік жүйеде де ол қарапайым және келесі теңдікпен анықталады:
| 
|
| 
|
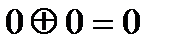
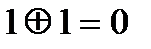
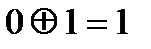
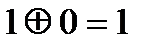
Тиімді кодтау
Кодтау барысында хабар көзінің статистикалық қасиетін ескере отырып, хабардың бір әріпін анықтау үшін екілік символдардың орташа санын минималдауға болады, ол кедергі болмаған жағдайда ақпарат өткізу уақытын азайтады.
Мұндай тиімді кодтау кедергісіз каналдарға арналған Шеннонның негізгі теоремасымен (№1 теорема) анықталады: Белгілі бір алфавиттің әріптерінен құралған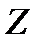 
-хабары 
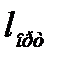әріпімен белгіленген екілік символдардың орташа саны, осы хабардың 
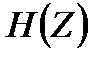энтропия көзіне қажет болғанынша жақын, бірақ бұдан кем емес, яғни 
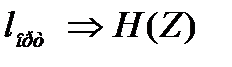(ескерту: 
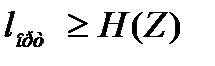) болатындай кодтауға болады.
Дата добавления: 2016-04-22; просмотров: 2155;