Базистік типін таңдау.

Базистік функциялар типін таңдау негізінен дискреттеу құрылғысының қиындық шектелуінің талап етілуімен және сигналды қалпына келтірумен анықталады. Алғашқы сигналды қалпына келтіру үшін 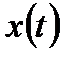таңдалуының жиынтығы кейбір көпмүшелерге сәйкес қойылады.

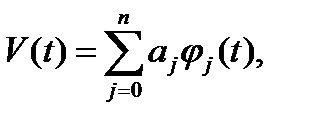
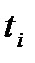есептеу нүктесіндегі мән 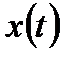функциясының мәнімен сәйкес келеді.

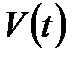туынды функциясы көбіне жақындағылармен сәйкес келеді, жалпы жағдайда олардан ерекшеленуі де мүмкін.

Дискреттеу есебінде қолданылатын функциялардың негізгі типтері: Фурье қатары, Котельников қатары, Чебышев полиномдары, Лежандр полиномдары, дәрежелік полиномдар, Уолта функциялары, Хаара функциялары, гипергеометриялық.

4) Жақындау принципі

Жақындау принципі бойынша әдістердің үш тобын бөліп алуға болады:

– интерполяциялық;

– экстраполяциялық;

– комбинациялық.

Экстраполяциялық әдістер дискреттеу кезінде сигналдың кідіруін талап етпейді, яғни нақты уақытта жұмыс істейтін, басқарушы жүйелерде қолданылуы мүмкін.

Интерполяциялық әдіс экстраполяциялық әдіспен салыстырғанда аралық есептеуді азайтуды қамтамасыз етеді, бірақ интерполяция интервалында сигналдың кідіруін талап етеді.

Интерполяциялық-экстрополяциялы әдістер үшін 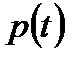жақын функциясын табу процедурасы екі этапқа бөлінеді. Бірінші этапта интерполяция әдістері болып 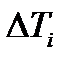бастапқы бөлігі үшін 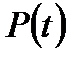жақындатылған функциясы табылады. Екінші этапта табылған функция 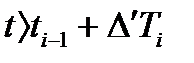мәні үшін энтрополяцияланады және бұл функциядан сигналдың ауытқуы тексеріледі.

Дискреттеу қадамын таңдау үшін сигналдардың әртүрлі модельдері қарастырылады және сәйкес есептеу критерийлері енгізіледі.

1) Санақ арасындағы интервал дисскреттелген сигналдың жиілік спектрі есебімен таңдалатын жиілік критериі;

2)Корреляциялы сигнал интервалдарымен санап шығарулар арасындағы интервалдар байланысын орнататын санап шығарудың корреляциялы критериі;

3)Сигналдың детерминирленген моделі үшін берілетін және сигналдың деңгейі мен бірінші туындысы бойынша квантты саты мәнімен санақ арасындағы интервалдар тәуелділігін орнататын, санап шығарулардың квантты критериі.