Неидеальный эксперимент. Формула Байеса

Рассмотрим случай неидеального эксперимента, который не приводит к выяснению в точности состояния природы, а лишь дает какие-то косвенные свидетельства в пользу тех или иных состояний. В общем случае эксперимент E приводит к появлению одного из k несовместных событий 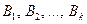. Причем вероятности этих событий (исходов эксперимента) зависят от условий, в которых проводится эксперимент. 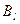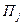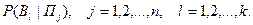Обозначим условную вероятность появления события в условиях через Будем считать, что эти вероятности нам известны.

После осуществления эксперимента E , давшего, например, исход 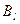, нам придется пересмотреть вероятности состояний природы. Они будут характеризоваться уже не прежними (априорными) вероятностями 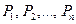, а новыми апостериорными вероятностями 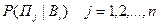, т.е. условными вероятностями состояний
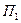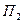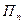, , …, при условии, что эксперимент дал результат 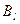. Этот пересчет осуществляется по формуле Байеса. Прежде чем привести формулу Байеса, напомним формулу полной вероятности. Эта формула позволяет определить вероятность события 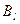, которое может наступить лишь при условии появления одного из событий
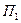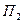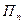, , …, , образующих полную группу несовместных событий:

,

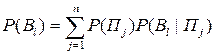где 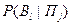– условная вероятность появления события 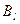при условии, что появилось событие .

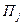Формула Байеса выводится из известной формулы для вероятности совместного наступления двух зависимых событий. Она может быть записана в двух вариантах:

.

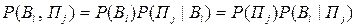Отсюда получаем:

.

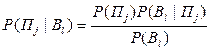Воспользовавшись для 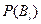формулой полной вероятности, получаем формулу Байеса в окончательном виде:

.

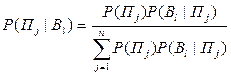Принятию окончательного решения может предшествовать многократный эксперимент. Тогда представление расчетов в виде одношаговой игры становится неудобным, и поэтому переходят к представлению расчетов в виде дерева решений.

Дерево решений – это древообразный граф, с вершинами которого сопоставляются возможные решения, сопутствующие события, утверждения и исходы. Ребра графа отражают логическую связь между этими элементами. Корнем дерева является вершина, обозначающая первое из принимаемых решений. Путь от начальной вершины дерева до вершины, отражающей конкретный исход, соответствует конкретной ситуации. Будем изображать вершины дерева, соответствующие анализируемым решениям, в виде прямоугольников, а все остальные вершины в виде овалов.