Задачи для самостоятельного решения. 1. Компания «Российский сыр» – небольшой производитель различных продуктов из сыра на экспорт
1. Компания «Российский сыр» – небольшой производитель различных продуктов из сыра на экспорт. Один из продуктов – сырная паста – поставляется в страны ближнего зарубежья. Генеральный директор должен решить, сколько ящиков сырной пасты следует производить в течение месяца. Вероятности того, что спрос на сырную пасту в течение месяца будет 6, 7, 8 или 9 ящиков, равны соответственно 0.1, 0.3, 0.5, 0.1.
Затраты на производство одного ящика равны 45 дол. Компания продает каждый ящик по цене 95 дол. Если ящик с сырной пастой не продается в течение месяца, то она портится и компания не получает дохода. Сколько ящиков следует производить в течение месяца?
2. Необходимо закупить уголь для обогрева дома. Количество хранимого угля ограничено и в течение холодного периода должно быть полностью израсходовано. Предполагается, что неизрасходованный зимой уголь в лето пропадает. Покупать уголь можно в любое время, однако летом он дешевле, чем зимой. Неопределенность состоит в том, что не известно, какой будет зима: суровой, тогда придется докупать уголь, или мягкой, тогда часть угля может остаться неиспользованной. Вероятности зим: мягкой – 0.35, обычной – 0.5, холодной – 0.15. Имеются следующие данные о количестве и ценах угля, необходимого зимой для отопления дома.
| Зима | Количество угля, т. | Средняя цена за 1 т. |
| Мягкая | ||
| Обычная | 7.5 | |
| Холодная |
Эти цены относятся к покупке угля зимой. Летом цены угля
6 у.е. за 1 т. Есть место для хранения запаса угля до 6 т., заготавливаемого летом. Если потребуется зимой докупить недостающее количество угля, докупка будет по зимним ценам. Сколько угля летом покупать на зиму?
3. АО «Фото и цвет» – небольшой производитель химических реактивов и оборудования, которые используются некоторыми фотостудиями при изготовлении 35-мм фильмов. Один из продуктов, который предлагает «Фото и цвет», – ВС-6. Президент АО продает в течение недели 11, 12 или 13 ящиков ВС-6. От продажи каждого ящика АО получает 35 дол. прибыли. Как и многие фотографические реактивы ВС-6 имеет малый срок годности. Поэтому, если ящик не продан к концу недели, он должен быть уничтожен. Каждый ящик обходится предприятию в 56 дол. Вероятности продать 11, 12 и 13 ящиков в течение недели равны соответственно 0.45, 0.35, 0.2. Найти оптимальное решение.
4. Компания, производящая стиральный порошок, работает в условиях свободной конкуренции. Порошок выпускается блоками, причем цена одного блока в будущем месяце является неопределенной: 10 р. с вероятностью 0.3, 15 р. с вероятностью 0.5, 20 р. с вероятностью 0.2. Полные затраты (ПЗ) на производство Q блоков стирального порошка определяются зависимостью ПЗ = 1000 + 5 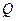 + 0.0025
+ 0.0025 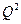 . Определить суточный выпуск продукции компании (в блоках), при котором среднесуточная прибыль будет максимальной.
. Определить суточный выпуск продукции компании (в блоках), при котором среднесуточная прибыль будет максимальной.
5. Спрос на некоторый товар, производимый монополистом, определяется зависимостью  , где j – достоверно неизвестный уровень дохода потребителей, p – цена товара. По оценкам экспертов, с вероятностью 0.6 j =2, а с вероятностью 0.4 j =4. Полные затраты на производство товара определяются зависимостью ПЗ =
, где j – достоверно неизвестный уровень дохода потребителей, p – цена товара. По оценкам экспертов, с вероятностью 0.6 j =2, а с вероятностью 0.4 j =4. Полные затраты на производство товара определяются зависимостью ПЗ =  . Сколько товара должен выпускать монополист и по какой цене продавать, чтобы максимизировать свою ожидаемую прибыль?
. Сколько товара должен выпускать монополист и по какой цене продавать, чтобы максимизировать свою ожидаемую прибыль?
6. Небольшая частная фирма производит косметическую продукцию для подростков. В течение месяца реализуется 15, 16 или 17 упаковок товара. От продажи каждой упаковки фирма получает 75 р. прибыли. Косметика имеет малый срок годности, поэтому, если упаковка не продана в месячный срок, она должна быть уничтожена. Поскольку производство одной упаковки обходится в 115 р., потери фирмы составляют 115 р., если упаковка не продана к концу месяца. Вероятность продать 15, 16 или 17 упаковок за месяц составляют соответственно 0.55, 0.1 и 0.35. Сколько упаковок косметики следует производить фирме ежемесячно? Какова ожидаемая стоимостная ценность этого решения? Сколько упаковок можно было бы производить при значительном продлении срока хранения косметической продукции?
7. Магазин «Молоко» продает в розницу молочные продукты. Директор магазина должен определить, сколько бидонов сметаны следует закупить у производителя для торговли в течение недели. Вероятности того, что спрос на сметану в течение недели будет 7, 8, 9 или 10 бидонов, равны соответственно 0.2, 0.2, 0.5 и 0.1. Покупка одного бидона сметаны обходится магазину в 70 р., а продается сметана по цене 110 р. за бидон. Если сметана не продается в течение недели, она портится, и магазин несет убытки. Сколько бидонов сметаны желательно приобретать для продажи? Какова ожидаемая стоимостная ценность этого решения?
Лабораторная работа № 9
Тема: статистические решения
Цель: научиться решать прикладные экономические задачи методами теории статистических решений и планирования эксперимента на основе дерева решений и с использованием пакета прикладных программ Qmwin.
Дата добавления: 2016-04-14; просмотров: 3110;
