Идеальный эксперимент
Рассмотрим случай идеального эксперимента E, приводящего к совершенно точному знанию состояния природы. Пусть задана матрица выигрышей 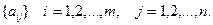 Пусть также известны вероятности
Пусть также известны вероятности  состояний природы
состояний природы 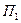 ,
, 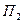 , …,
, …, 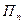 , а затраты на проведение эксперимента равны C. Если не проводить эксперимента, то нужно выбрать стратегию с максимальным средним выигрышем:
, а затраты на проведение эксперимента равны C. Если не проводить эксперимента, то нужно выбрать стратегию с максимальным средним выигрышем:
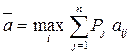 .
.
Теперь предположим, что мы провели эксперимент E и точно выяснили действительное состояние природы. Если это состояние 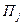 , то надо применять стратегию, для которой достигается
, то надо применять стратегию, для которой достигается
 .
.
Но нам надо заранее решить, будем ли мы производить эксперимент E или нет, и нам неизвестно, какое состояние на самом деле имеет место, а значит, и какой будет выигрыш. В связи с этим осредним возможный средний выигрыш:
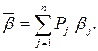
Таким образом, потребность в эксперименте должна определяться по правилу:
 .
.
Представим неравенство в более удобном виде. Для этого раскроем  , C перенесем в левую часть, а
, C перенесем в левую часть, а  в развернутом виде – в правую часть неравенства:
в развернутом виде – в правую часть неравенства:
 .
.
Внесем минус под максимум, заменяя одновременно максимум на минимум. Далее, объединяя суммы в правой части, получаем:
 .
.
Нетрудно видеть, что это равносильно неравенству:
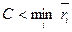 .
.
Дата добавления: 2016-04-14; просмотров: 782;
