Формула сферического зеркала
 Найдем связь между расстоянием d светящейся точки от зеркала, расстоянием f изображения этой точки от зеркала и радиусом R сферы, частью которой является зеркало. Рассмотрим сначала вогнутое зеркало (рис. 3.26).
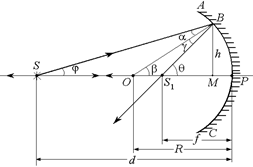
Найдем связь между расстоянием d светящейся точки от зеркала, расстоянием f изображения этой точки от зеркала и радиусом R сферы, частью которой является зеркало. Рассмотрим сначала вогнутое зеркало (рис. 3.26).
Рис. 3.26
Пусть светящаяся точка S расположена на главной оптической оси ОР вогнутого зеркала. Из точки S на зеркало падает множество лучей, один из которых SP после отражения в точке Р идет вдоль главной оси. Для этого луча угол падения, а следовательно, и угол отражения равен нулю, так как радиус ОР является перпендикуляром (нормалью) к сферической поверхности. Построим ход произвольного луча SB, вышедшего из точки S и отразившегося от зеркала в точке В. Будем рассматривать лишь узкие, приосевые пучки лучей. Тогда точка В окажется на небольшом расстоянии h от главной оптической оси (h << R).
При выполнении этого условия падающий луч SB и отраженный луч BS1, а также радиус ОВ, проведенный в точку падения В, составляют с главной осью углы столь малые, что их синусы можно заменить тангенсами, а также самими углами, выраженными в радианах. В точке S1 луч BS1 пересечется с лучом PS1, отразившимся в полюсе зеркала. Если остальные лучи после отражения также пройдут через точку S1, то эта точка будет являться действительным изображением точки S.
Радиус ОВ перпендикулярен к отражающей поверхности. По закону отражения угол падения a равен углу отражения g. Для треугольника SBO можно по теореме о внешнем угле треугольника записать:
b = a + j. (1)
Точно так же для треугольника OBS1:
q = b + g. (2)
Учитывая, что g = a, из (2) получим
q = b + a. (3)
Найдем связь между углами g, b и q. Для этого выразим угол a из (1) и подставим в (3):
a = b – j Þ q = b + (b – j) Þ
q + j = 2b. (4)
Теперь рассмотрим прямоугольные треугольники SBM, OBM и S1ВМ и выразим значения углов j, b и q через катеты этих треугольников:
DSBM: 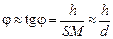 ;
;
DОBM: 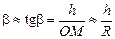 ;
;
DS1BM: 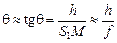 .
.
Подставляя эти значения g, b и q в формулу (4), получим
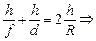
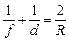 . (3.2)
. (3.2)
Формула (3.2) называется формулой сферического зеркала.
Поскольку h не входит в формулу (3.2), то получается, что любой луч, вышедший из точки S и отразившийся от зеркала, пройдет через точку S1, т.е. точка S1 является действительным изображением точки S.
Если в формуле (3.2) положить d ® ¥, т.е. источник бесконечно удаляется от зеркала, и лучи, падающие на зеркало, параллельны главной оптической оси (рис. 3.27, а), то из формулы (3.2) получим
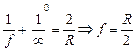 .
.
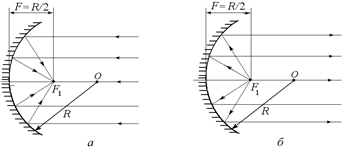
Рис. 3.27
Эта величина является фокусным расстоянием зеркала, т.е. расстоянием зеркала до главного фокуса, и обозначается буквой F:
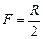 .
.
Другими словами, фокусное расстояние равно половине радиуса! Мы с вами теоретически обосновали формулу (3.1), которую в начале параграфа приняли к сведению как экспериментальный факт. С учетом того, что F = R/2, формула (3.2) имеет вид
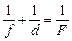 . (3.3)
. (3.3)
Из принципа обратимости световых лучей следует, что если в главном фокусе вогнутого зеркала расположить точечный источник, то лучи, выходящие из этого источника, после отражения от зеркала будут параллельны главной оптической оси (рис. 3.27, б).
А вот когда все вроде бы стало ясно, давайте посмотрим, как пойдут отраженные от вогнутого зеркала лучи в случае, показанном на рис. 3.27, б), если рассматривать не только малые, а все возможные углы, которые падающие лучи составляют с главной оптической осью.
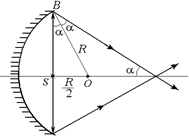 Рис. 3.28
Рис. 3.28
|
Рассмотрим луч SB, падающий на зеркало из точки S, расположенной в главном фокусе (рис. 3.28). Луч SB составляет с главной оптической осью угол 90°. В прямоугольном DSBO катет SO = R/2, а гипотенуза ОВ = R, следовательно, ÐSBO = a лежит против катета, который в 2 раза меньше гипотенузы, а значит, a = 30°. Тогда, как видно из рис. 3.28, отраженный луч ВО вовсе не параллелен главной оптической оси, а пересекает ее под углом BS1О = 90° – 2×30° = 30°.
Читатель: Из формулы (3.3) следует, что 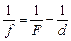 , значит, если d < F, то
, значит, если d < F, то 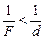 и
и 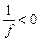 , т.е. f < 0. Что бы это значило?
, т.е. f < 0. Что бы это значило?
Автор: Если f < F, значит, источник находится между фокальной плоскостью и зеркалом (см. рис. 3.12). В этом случае получится мнимое изображение, которое находится за зеркалом.
Для удобства дальнейших расчетов договоримся, что величину f в формуле (3.3) будем считать алгебраической. Если f > 0, то изображение действительное, а если f < 0 – изображение мнимое.
Задача 3.6. Вогнутое зеркало с радиусом кривизны R = 1,0 м дает мнимое изображение предмета, расположенное на расстоянии 3,0 м от зеркала. На каком расстоянии d от зеркала находится предмет?
| R = 1,0 м f = –3,0 м | Решение. Поскольку изображение мнимое, то f = = – 3,0 м < 0.
Воспользуемся формулой сферического зеркала (3.3) 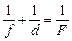 и найдем d: и найдем d:
|
| d = ? | |
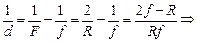
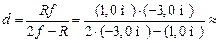
» 0,43 м.
Ответ: 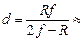 0,43 м.
0,43 м.
СТОП! Решите самостоятельно: А7, А8, В9, С4, С5, D1.
Читатель: А как быть, если зеркало выпуклое? Ведь формула (3.3) получена для вогнутого зеркала?
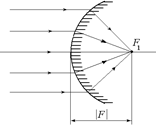 Рис. 3.29
Рис. 3.29
|
Автор: Когда зеркало выпуклое, то главный фокус расположен за зеркалом (рис. 3.29). Можно показать (мы это делать не будем), что формула сферического зеркала в этом случае также будет справедлива, если величину F в формуле (3.3) взять со знаком «минус». А это значит, что величину F в формуле (3.3) тоже следует рассматривать как величину алгебраическую:
1) если зеркало вогнутое, то 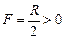 ;
;
2) если зеркало выпуклое, то 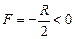 .
.
Задача 3.7. Радиус кривизны выпуклого зеркала R = 1,6 м. На каком расстоянии d перед зеркалом должен находиться предмет, чтобы его изображение получилось в п = 1,5 раза ближе к зеркалу, чем сам предмет?
| R = 1,6 м п = 1,5 | Решение. Изображение в выпуклом зеркале всегда мнимое (см. рис. 3.14), поэтому f < 0. Если d – это расстояние от зеркала до предмета, а |f| – расстояние от зеркала до изображения, то согласно условию зада- |
| d = ? | |
чи 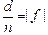 , а с учетом того, что f < 0, получаем
, а с учетом того, что f < 0, получаем
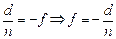 . (1)
. (1)
Формула зеркала в данном случае имеет вид
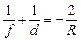 . (2)
. (2)
Подставим (1) в (2):
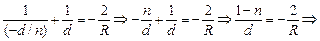
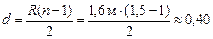 м.
м.
Ответ: 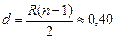 м.
м.
СТОП! Решите самостоятельно: А9, А10, В10, С6, D2.
Мнимый источник
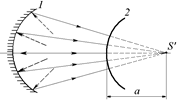 Рис. 3.30
Рис. 3.30
|
Читатель: Допустим, в вогнутом зеркале 1 получено действительное изображение (рис. 3.30). Если мы поставим второе сферическое зеркало (выпуклое или вогнутое) на пути сходящихся лучей, то, наверное, эти лучи, отразившись от второго зеркала, дадут изображение (действительное или мнимое). Как нам тогда узнать, где находится это изображение?
Автор: Это случай так называемого мнимого источника. То есть за зеркалом 2 пересекаются продолжения падающих на него лучей. В этом случае тоже можно применять формулу сферического зеркала (3.3): 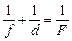 , только величину d здесь следует взять равной расстоянию от зеркала до мнимого источника со знаком «минус», т.е. d = –a (см. рис. 3.30).
, только величину d здесь следует взять равной расстоянию от зеркала до мнимого источника со знаком «минус», т.е. d = –a (см. рис. 3.30).
Теперь мы уже можем сформулировать «правило знаков» для сферического зеркала в самом общем случае. Итак: для любого сферического зеркала в любой ситуации справедливо
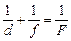 ,
,
где d > 0, если источник действительный; d < 0, если источник мнимый; f > 0, если изображение действительное; f < 0, если изображение мнимое; 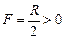 , если зеркало вогнутое;
, если зеркало вогнутое; 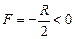 , если зеркало выпуклое.
, если зеркало выпуклое.
Задача 3.8. Сходящиеся лучи падают на выпуклое зеркало так, что их продолжения пересекаются в точке, находящейся на расстоянии 0,40 м за зеркалом. После отражения от зеркала лучи расходятся таким образом, что их продолжения пересекаются в точке, отстоящей от зеркала на расстоянии 1,6 м. Обе точки пересечения лежат на главной оптической оси зеркала. Найти фокусное расстояние F зеркала.
| d = –0,40 м f = –1,6 м | Решение. В данном случае мы имеем мнимый источник, поэтому d < 0, и мнимое изображение, поэтому f < 0. Найдем фокусное расстояние: |
| F = ? | |
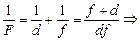
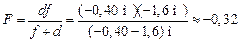 м.
м.
Ответ: 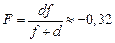 м.
м.
СТОП! Решите самостоятельно: А11, А12, В11, С7, D3.
Дата добавления: 2016-04-11; просмотров: 13016;
