Область наблюдения предмета

В выпуклом зеркале

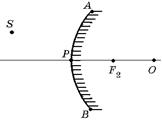Рис. 3.34

Задача 3.12.Укажите на рисунке область, из которой можно видеть изображение точки S в выпуклом зеркале (рис. 3.34). Главный фокус и центр зеркала заданы.

Решение. 1. Построим изображение точки S. Для этого пустим на зеркало два луча: луч 1, параллельный главной оптической оси, и луч 2, продолжение которого проходит через центр зеркала – точку O (рис. 3.35).

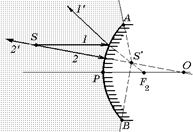Рис. 3.35

Тогда продолжение отраженного луча 1¢ проходит через главный фокус зеркала – точку F₂, а отраженный луч 2¢ совпадает с падающим лучом 2. Пересечение продолжений отраженных лучей 1¢ и 2¢ дают изображение точки S – точку S¢.

2. Область наблюдения изображения – это область, в которую попадают лучи, исходящие от источника и отраженные от зеркала. Чтобы получить область наблюдения на рисунке, надо провести прямые из точки S¢ через края зеркала – точки А и В. Тогда область, ограниченная самим зеркалом и прямыми S'А и S'В, и является областью, из которой можно наблюдать мнимое изображение – точку S¢.

Заметим, что область наблюдения предмета в выпуклом зеркале больше, чем область наблюдения того же предмета в плоском зеркале.

Чтобы было понятно, почему это так, покажем область наблюдения изображения точки S, находящейся на таком же расстоянии от плоского зеркала, на каком находится точка S от выпуклого зеркала на рис. 3.34. Построение показано на рис. 3.36.

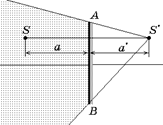Рис. 3.36

Из рисунка видно, что область наблюдения в плоском зеркале гораздо ýже, чем в выпуклом. Объясняется это тем, что в выпуклом зеркале мнимое изображение находится очень близко к зеркалу – не дальше его фокальной плоскости. В плоском зеркале расстояние от плоскости зеркала до мнимого изображения равно, как мы знаем, расстоянию от зеркала до предмета: а = а¢.

Задача 3.13. Светящаяся точка находится на главной оптической оси вогнутого зеркала на одинаковых расстояниях от зеркала и его фокуса. Перпендикулярно к оси зеркала расположен экран, центр которого совпадает с оптическим центром зеркала. Во сколько раз диаметр светлого круга на экране превышает диаметр зеркала?

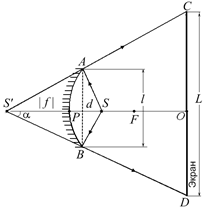Рис. 3.37

она дает мнимое изображение S¢, а лучи, падающие на экран, можно считать исходящими из мнимого изображения S¢ точки S. Изображение мнимое, поэтому f < 0.

Воспользуемся формулой зеркала 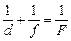, где 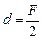, получим

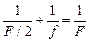Þ ,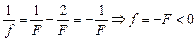

соответственно | f | = F (см. рис. 3.37).

Рассмотрим подобные треугольники S¢AB и S¢CD. Из их подобия следует

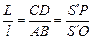. (1)

(Мы считаем лучи S¢C и S¢D параксиальными, поэтому точку Р можно приближенно считать лежащей на отрезке АВ.)

Поскольку по условию задачи О – центр зеркала, то РО = R = = 2F. Как видно из рис. 3.37, S¢P = | f | = F, тогда

S¢О = S¢Р + РО = F + 2F = 3F.

Подставляя значения S¢О и S¢Р в (1), получим

.

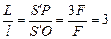Ответ: .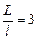

СТОП! Решите самостоятельно: С14–С16, D6.