ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ. А1. Как в солнечный день определить приблизительно радиус кривизны вогнутого зеркала?

Задачи легкие

А1. Как в солнечный день определить приблизительно радиус кривизны вогнутого зеркала?

А2. Постройте дальнейший ход луча, падающего на вогнутое зеркало (рис. 3.38).

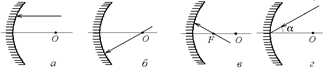
Рис. 3.38

А3. Постройте изображения предметов в вогнутом зеркале (рис. 3.39).

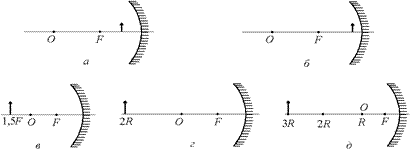
Рис. 3.39

А4. Фокусное расстояние вогнутого зеркала 30 см. Где будет расположено изображение свечи, находящейся от зеркала на расстоянии 60 см. (Решить задачу построением.)

А5. Постройте дальнейший ход луча, падающего на выпуклое зеркало (рис 3.40).

Рис. 3.40

А6. Постройте изображение предмета в выпуклом зеркале (рис. 3.41).

Рис. 3.41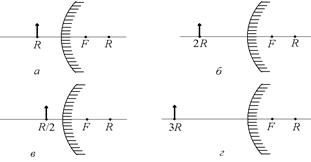

А7. Расстояние от предмета до вогнутого зеркала d = 0,5 м, расстояние от зеркала до изображения f = 2 м. Найти радиус кривизны R зеркала.

А8. Расстояние от точечного источника света до вогнутого зеркала d = 2R, где R – радиус кривизны зеркала. Источник находится на главной оптической оси зеркала. Где расположено его изображение? Построить ход лучей.

А9. Предмет находится на расстоянии d = 5,0 м от выпуклого зеркала с радиусом кривизны R = 1,5 м. На каком расстоянии f от зеркала находится изображение предмета? Какое это изображение?

А10.Изображение источника света получено с помощью выпуклого зеркала на расстоянии 60 см от зеркала. На каком расстоянии d от зеркала расположен источник, если фокусное расстояние зеркала F = – 90 cм?

А11. Сходящиеся лучи падают на вогнутое зеркало с радиусом кривизны R = 60 см так, что их продолжения пересекаются на оси зеркала в точке S на расстоянии а = 15 см за зеркалом. На каком расстоянии от зеркала сойдутся эти лучи после отражения от зеркала? Будет ли точка их пересечения действительной?

А12. Вогнутое зеркало поставлено против сходящегося пучка лучей так, что точка, где лучи пересекались, осталась за зеркалом на расстоянии 20 см от его полюса. Отраженные от зеркала лучи сошлись в одну точку на расстоянии, равном 1/5 фокусного расстояния зеркала. Найти радиус кривизны зеркала.