Сложение гармонических колебаний. Гармоническое колебание как проекция вектора,

Гармоническое колебание как проекция вектора,

Вращающегося с постоянной угловой скоростью

Наиболее просто складываются гармонические колебания одинаковых частот. Предварительно рассмотрим проекцию вращающегося вектора.

Рис. 16.16

Пусть вектор 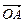вращается с посто­янной угловой скоростью w вокруг оси, проходящей через точку О (рис. 16.16).

Модуль вектора 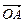обозначим через а. В начальный момент времени t = 0 век­тор образует с осью х угол j₀. В даль­нейшем при равномерном вращении угол между вектором 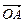и осью х ли­нейно растет со временем:

j = wt + j₀. (16.14)

Проекция вектора 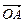на ось X равна:

х = a cosj = a cos(wt + j₀). (16.15)

Одновременно проекция этого вектора на ось Y оказывается равной

у = a sin(wt + j₀).

Мы получили простой, но важный результат.

Проекция вектора, вращающегося с постоянной скоро­стью, совершает гармонические колебания с частотой, рав­ной угловой скорости вращения вектора. Амплитуда этих колебаний равна модулю вектора, а начальная фаза равна углу, образованному вектором 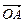с осью координат X в на­чальный момент времени.