Индуктивное сопротивление
Рассмотрим экспериментальные факты.
  а б
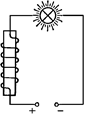
Рис. 16.12
а б
Рис. 16.12
|
1. Включим в цепь постоянного тока последовательно электрическую лампу и катушку индуктивности (рис. 16.12, а).
Лампочка будет гореть практически тем же накалом, как при отсутствии катушки (рис. 16.12, б), т.е. постоянный ток как бы «не замечает» катушку. И это неудивительно: если проволока достаточно толстая, то активное сопротивление катушки очень мало.
 Рис. 16.13
Рис. 16.13
|
2. Если же на последовательно соединенные лампочку и катушку подать переменное напряжение с действующим значением, равным постоянному напряжению, то накал лампочки значительно уменьшится (рис. 16.13). А это значит, что действующее значение силы тока существенно меньше значения постоянного тока в первом случае.
3. Если теперь постепенно вытягивать из катушки железный сердечник, то накал лампы будет возрастать, т.е. уменьшая индуктивность катушки, мы увеличиваем действующее значение силы тока в цепи.
Автор: Как же объяснить эти опыты?
Читатель: Я думаю, все дело в самоиндукции. Ведь ток в цепи быстро меняется, в катушке возникает вихревое электрическое поле, которое мешает нарастанию тока в цепи. Поэтому действующее значение силы тока становится тем меньше, чем больше индуктивность катушки.
Автор: Вы правы. А как будет влиять на действующее значение силы тока частота тока?
Читатель: Чем больше частота, тем больше ЭДС самоиндукции, поэтому с увеличением частоты сила тока будет убывать.
Автор: Верно. А теперь попробуем получить зависимость тока от времени в цепи, состоящей только из источника переменного напряжения и катушки индуктивности.
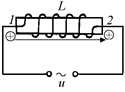 Рис. 16.14
Рис. 16.14
|
Пусть на катушку индуктивности (рис. 16.14) подается переменное напряжение, которое меняется по закону u = U0coswt. Будем считать, что активное сопротивление катушки пренебрежимо мало.
Выясним, как связаны между собой напряжение на концах u(t) и ЭДС самоиндукции ℰis(t) в данный момент времени t.
Заметим, что внутри катушки как бы «сталкиваются лбами» два электрических поля: поле кулоновских сил, созданное источником, и вихревое электрическое поле, которое возникает из-за изменения магнитного поля, созданного током катушки.
Поставим вопрос: может ли результирующая напряженность электрического поля в катушке быть отличной от нуля? (Сопротивление катушки мы считаем равным нулю.)
Читатель: Если предположить такое, то при перемещении единичного положительного заряда из точки 1 в точку 2 (см. рис. 16.14) его скорость должна либо увеличиться (если  ), либо уменьшиться (если
), либо уменьшиться (если 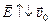 ). Но это бы означало, что сила тока различна в разных точках цепи!
). Но это бы означало, что сила тока различна в разных точках цепи!
Автор: Верно! Значит,  . А это значит, что работа, которую совершают над единичным положительным зарядом при переносе его из точки 1 в точку 2 кулоновские силы, в точности равна по величине и противоположна по знаку работе, которую совершают над зарядом силы вихревого поля. Следовательно, ℰis(t) = – u(t).
. А это значит, что работа, которую совершают над единичным положительным зарядом при переносе его из точки 1 в точку 2 кулоновские силы, в точности равна по величине и противоположна по знаку работе, которую совершают над зарядом силы вихревого поля. Следовательно, ℰis(t) = – u(t).
Теперь попробуем найти зависимость тока от времени i(t). Поскольку u(t) = U0coswt, то ℰis(t) = –U0coswt.
Из закона Фарадея известно, что ℰis = –Li¢(t), поэтому
–Li¢(t) = –U0coswt Þ 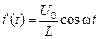 .
.
Чтобы найти i(t), найдем первообразную функции  :
:
 .
.
Константа интегрирования С находится из начального значения силы тока. Если i(0) = 0, то  , значит, С = 0,
, значит, С = 0, 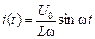 . Итак, запомним:
. Итак, запомним:
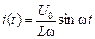 . (16.10)
. (16.10)
Тогда амплитудное значение тока
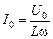 . (16.11)
. (16.11)
С учетом того, что  ,
, 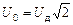 , можем записать
, можем записать
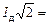
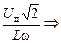
Iд = 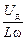 . (16.11а)
. (16.11а)
Величину Lw называют индуктивным сопротивлением
XL = wL. (16.12)
Тогда для действующих значений тока и напряжения выполняется закон Ома
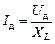 . (16.13)
. (16.13)
Аналогичное равенство справедливо и для амплитудных значений тока и напряжения
 . (16.13а)
. (16.13а)
Заметим, что если w = 0 (т.е. ток постоянный), то XL = 0: постоянному току катушка индуктивности не оказывает сопротивления. Если L = 0, то XL = 0, т.е. если индуктивность катушки очень мала, то ЭДС самоиндукции также очень мала, и катушка никак не может мешать переменному току.
 Рис. 16.15
Рис. 16.15
|
Изобразим графически зависимости i(t) и u(t) (рис. 16.15). Видим, что в данном случае ток опережает напряжение на p/2. В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю. В момент, когда напряжение становится равным нулю, сила тока максимальна по модулю.
Замечание. Для мгновенных значений тока и напряжения закон Ома не применим. В самом деле, в момент t = 0 iL(0) = 0, а uL(0) = = U0. Это противоречит закону Ома.
СТОП! Решите самостоятельно: А9, А10, В18–В21, С6.
Задача 16.6. Найти индуктивность катушки, если амплитуда напряжения на ее концах U0 = 160 В, амплитуда тока в ней I0 = 10 А и частота тока n = 50 Гц.
| U0 = 160 В I0 = 10 А n = 50 Гц | Решение.
 Þ I0×2pnL = U0 Þ Þ I0×2pnL = U0 Þ
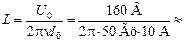 0,051 Гн. 0,051 Гн.
|
| L = ? | |
Ответ: 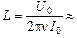 0,051 Гн.
0,051 Гн.
СТОП! Решите самостоятельно: А11, А12, В22.
Дата добавления: 2016-04-11; просмотров: 1128;
