Резонанс напряжений. При изучении вынужденных механических колебаний мы познакомились с важным явлением – резонансом

При изучении вынужденных механических колебаний мы познакомились с важным явлением – резонансом. Резо­нанс наблюдается в том случае, когда собственная час­тота колебаний системы совпадает с частотой внешней силы. При малом трении происходит резкое увеличение амплитуды установившихся вынужденных колебаний.

Амплитуда силы тока при вынужденных колебаниях в кон­туре, совершающихся под действием внешнего гармонически изменяющегося напряжения, определяется формулой (16.40)

.

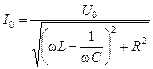При фиксированном напряжении и заданных значениях R, L и С амплитуда силы тока достигает максимума при частоте w, удовлетворяющей соотношению

. (16.47)

Знаменатель в формуле (16.40) становится при этом минималь­ным, и амплитуда силы тока достигает максимального значения

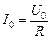. (16.48)

Эта амплитуда особенно велика при малом R.

Из уравнения (16.47) можно определить циклическую час­тоту переменного тока, при которой сила тока максимальна:

. (16.49)

Эта частота совпадает с частотой свободных колебаний в колебательном контуре с малым активным сопротивлением.

Резкое возрастание амплитуды вынужденных колебаний силы тока в колебательном контуре с малым активным сопротивлением происходит при совпадении частоты внеш­него переменного напряжения с собственной частотой коле­бательного контура. В этом состоит явление резонанса в электрическом колебательном контуре.

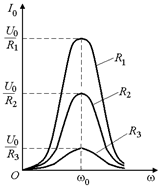Рис. 16.36

Резонанс выражен тем отчетливее, чем меньше энергетические потери в цепи, т. е. чем меньше сопротивление R. При R ® 0 резонансное значение силы тока неограниченно возраста­ет: I_рез ® ¥. Наоборот, с увеличени­ем R максимальное значение тока уменьшается, и при больших R гово­рить о резонансе уже не имеет смыс­ла. Зависимость амплитуды силы то­ка от частоты при различных сопро­тивлениях показана на рис. 16.36 (r₁ < r₂ < r₃).

Одновременно с ростом силы то­ка при резонансе резко возрастают напряжения на конден­саторе и катушке индуктивности. Эти напряжения ста­новятся одинаковыми и во много раз превосходят внешнее напряжение.

Действительно,

U_{0С рез} = I_{0 рез} = I_{0 рез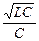} = I_{0 рез} ;

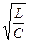U_{0L рез} = I_{0 рез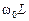} = I_{0 рез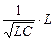} = I_{0 рез} .

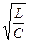Внешнее напряжение связано с резонансной силой тока так:

U₀ = I_{0 рез} Z = I_{0 рез}R (так как Z = R).

Если R<< 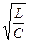, то U_{0С рез} = U_{0L рез} >> U₀.

При резонансе сдвиг фаз между током и напряжением становится согласно формуле (16.46) равным нулю. Наглядно это можно пояснить так. Колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. Резонансные амплитуды этих напряжений одинаковы. В результате напряжения на катушке и конденсаторе пол­ностью компенсируют друг друга (u_L = = –u_С),и падение напря­жения происходит только на участке с активным сопротивле­нием.

Рис. 16.37

Явление электрического резонанса используется, в част­ности, при осуществлении радиосвязи. Радиоволны от различ­ных передающих станций возбуждают в антенне радиоприем­ника переменные токи различных частот (рис. 16.37),так как каждая передающая радиостанция работает на своей частоте. С антенной индуктивно свя­зан колебательный контур. Вследствие элек­тромагнитной индукции в контурной катуш­ке возникают переменные ЭДС соответствую­щих частот и вынужденные колебания силы тока этих же частот. Но только при резонансе колебания силы тока в контуре и напряжения на конденсаторе контура будут значительны­ми. Имея это в виду, говорят, что из колебаний всех частот, возбужденных в антенне, контур выделяет только колебания, частота которых равна собственной частоте контура. Настройка контура на нужную частоту w₀ обыч­но осуществляется путем изменения емкости конденсатора. В этом состоит настройка радиоприемника на определенную радиостанцию.

В некоторых случаях резонанс в электрической цепи мо­жет принести большой вред. Если цепь не рассчитана на рабо­ту в условиях резонанса, то возникновение резонанса приве­дет к аварии. Чрезмерно большие токи могут перегреть прово­да. Большие напряжения приведут к пробою изоляции.

СТОП! Решите самостоятельно: В34.

Задача 16.11. Цепь, состоящая из последовательно соединен­ных резистора, катушки индуктивности и конденсатора, на­ходится под напряжением 1,1кВ. Активное сопротивление цепи 100Ом. При резонансе индуктивное и емкостное со­противления равны по 1000 Ом.Каковы сила тока в цепи и напряжение на конденсаторе? Почему при резонансе в та­кой последовательной цепи возможен пробой конденсатора?

Uд = 1,1 кВ = = 1,1×103 В R = 100 Ом XL = 1000 Ом XC = 1000 Ом	Решение. Поскольку в цепи наступил резонанс, полное сопротивление (импеданс) Z = R. Тогда 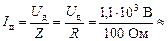11 А. Действующее значение напряжения на емкости равно UСд = IдХС = 11 А × 1000 Ом » 11 кВ.
Iд = ? UСд = ?

Как видим, действующее значение напряжения на конденсаторе очень велико: 11 кВ! Не забудем, что амплитуда значения напряжения еще больше: U_0С = U_Сд 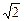. При таком большом напряжении, которое в 10 раз превосходит напряжение на входе (1,1 кВ) вполне возможен пробой конденсатора.

Ответ: I_д » 11 А; U_Сд» 11 кВ.

СТОП! Решите самостоятельно: В35, С20, С21.