Вычисление напряжений при колебаниях.
Упругая система, выведенная каким-либо путем из равновесия, приходит в колебательное движение. Колебания происходят около положения упругого равновесия, при котором в нагруженной системе имели место статические деформации 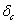 и соответствующие им статические напряжения
и соответствующие им статические напряжения 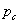 (
( 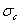 или
или 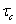 — в зависимости от вида деформации). При колебаниях к статическим деформациям добавляются динамические, зависящие от вида колебательного движения и от величины размаха (амплитуды) колебаний. В связи с этим изменяются и напряжения
— в зависимости от вида деформации). При колебаниях к статическим деформациям добавляются динамические, зависящие от вида колебательного движения и от величины размаха (амплитуды) колебаний. В связи с этим изменяются и напряжения 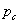 . Таким образом, при расчете колеблющейся системы на прочность необходимо уметь вычислять динамические добавки к статическим деформациям и соответствующим им напряжениям.
. Таким образом, при расчете колеблющейся системы на прочность необходимо уметь вычислять динамические добавки к статическим деформациям и соответствующим им напряжениям.
Во многих случаях характер колебаний системы может быть определен одной какой-нибудь величиной (одной координатой). Такие системы называются системами с одной степенью свободы; таковы, например, растянутая или сжатая незначительного веса пружина с грузом на конце, совершающая продольные колебания; небольшого (сравнительно с грузом Q) собственного веса балка, изображенная на Рис.2, колеблющаяся в направлении, перпендикулярном к ее оси, и т. п.

Рис.2. Динамическая модель колебаний системы с одной степенью свободы.
При колебаниях систем с одною степенью свободы полные деформации системы в каком либо сечении могут быть найдены путем сложения статической деформации с добавочной деформацией при колебаниях. Для проверки прочности системы, очевидно, необходимо найти наиболее опасное сечение с наибольшей в процессе колебаний суммарной величиной деформации. В простейших случаях для этого потребуется сложить наибольшую статическую деформацию 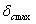 с наибольшей амплитудой колебаний А, т. е.
с наибольшей амплитудой колебаний А, т. е.
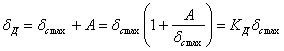
Пока система деформируется в пределах упругости, напряжения пропорциональны деформациям. Поэтому
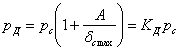
где
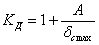
— коэффициент динамичности при колебаниях. Условие прочности в этом случае должно иметь такой вид:
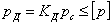
Таким образом задача нахождения динамических напряжений и проверки прочности при колебаниях может быть сведена к определению статических напряжений и коэффициента динамичности 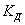 . Так как последний зависит от величины А, то нужно уметь определять наибольшее значение амплитуды колебаний в разных случаях.
. Так как последний зависит от величины А, то нужно уметь определять наибольшее значение амплитуды колебаний в разных случаях.
Как известно, дифференциальное уравнение движения колеблющегося груза Q в случае свободных колебаний можно представить в виде уравнения равновесия, в котором кроме внешней силы (веса груза Q) и силы упругого сопротивления системы учитывается также и сила инерции:
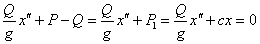
| (1) |
Здесь х — координата, полностью определяющая положение груза Q во время колебаний; Р — полное упругое сопротивление системы при колебаниях; 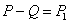 — так называемая восстанавливающая сила (добавочное упругое усилие, возникающее в системе в результате перемещения точки приложения груза Q на расстояние х при колебаниях), которую в пределах упругости можно считать пропорциональной координате х (
— так называемая восстанавливающая сила (добавочное упругое усилие, возникающее в системе в результате перемещения точки приложения груза Q на расстояние х при колебаниях), которую в пределах упругости можно считать пропорциональной координате х ( 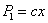 ); с — коэффициент пропорциональности, представляющий собой усилие, необходимое для того, чтобы вызвать равную единице статическую деформацию системы в направлении действия груза Q. Если статическая деформация от груза Q равна
); с — коэффициент пропорциональности, представляющий собой усилие, необходимое для того, чтобы вызвать равную единице статическую деформацию системы в направлении действия груза Q. Если статическая деформация от груза Q равна 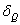 , то
, то 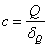 .
.
Решение уравнения (1) приводит к таким формулам для вычисления частоты 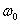 и периода
и периода 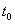 свободных колебаний:
свободных колебаний:
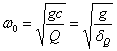 и
и 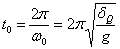
Свободные колебания невесомого тела суть простые гармонические колебания с частотой (периодом), равной частоте (периоду) колебаний математического маятника, длина которого равна статической деформации системы от груза Q. Так, например, если груз Q растягивает призматический стержень,
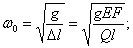
при изгибе балки на двух шарнирных опорах грузом Q посредине пролета
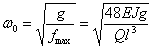
и т.д.
Если на упругую систему, кроме груза Q и силы упругого сопротивления системы Р, в том же направлении действует периодически меняющаяся возмущающая сила S и сила сопротивления среды R, то дифференциальное уравнение движения груза Q при колебаниях также может быть представлено в виде уравнения равновесия, подобного уравнению (1):
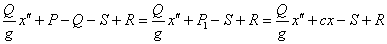
| (2) |
Силу сопротивления среды R на практике в довольно большом числе случаев можно считать пропорциональной первой степени скорости колебательного движения, т. е. 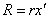 . Если возмущающая сила S меняется по синусоидальному закону:
. Если возмущающая сила S меняется по синусоидальному закону:
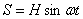 ,
,
где 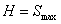 , а
, а 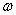 — частота возмущающей силы, то уравнение (2) может быть переписано так:
— частота возмущающей силы, то уравнение (2) может быть переписано так:
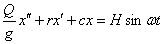
или
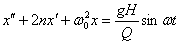
| (3) |
Здесь 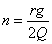 — так называемый коэффициент затухания колебаний,
— так называемый коэффициент затухания колебаний,
a 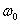 — найденная выше частота свободных колебаний системы, возникающих при отсутствии как возмущающей силы S так и силы сопротивления R.
— найденная выше частота свободных колебаний системы, возникающих при отсутствии как возмущающей силы S так и силы сопротивления R.
Решение уравнения (3) приводит к такому выражению для амплитуды А вынужденных колебаний при наличии сил сопротивления:
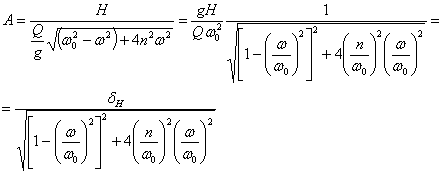
Здесь
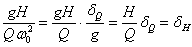
— статическая деформация системы от наибольшей величины возмущающей силы S ( 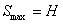 ). Отношение амплитуды вынужденных колебаний А к величине деформации
). Отношение амплитуды вынужденных колебаний А к величине деформации 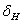 называется коэффициентом нарастания колебаний
называется коэффициентом нарастания колебаний 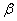 :
:
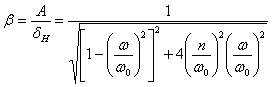
Таким образом, формула (35.21) для динамического коэффициента 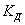 получает теперь такой вид:
получает теперь такой вид:
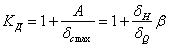
В этом выражении не учтена амплитуда собственных колебаний системы, которая может иметь сколько-нибудь существенное значение лишь в самом начале процесса колебаний; при наличии сил сопротивления она довольно быстро уменьшается с течением времени.
На рис.3 приведены графики изменения коэффициента нарастания колебаний 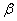 в зависимости от величины отношения
в зависимости от величины отношения 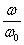 при разных значениях коэффициента затухания колебаний n ( отношения
при разных значениях коэффициента затухания колебаний n ( отношения 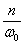 ). Если частота изменения возмущающей силы близка к частоте свободных колебаний системы, т. е.
). Если частота изменения возмущающей силы близка к частоте свободных колебаний системы, т. е. 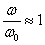 , и если величина коэффициента затухания колебаний сравнительно невелика, то знаменатели формул и для A и
, и если величина коэффициента затухания колебаний сравнительно невелика, то знаменатели формул и для A и 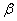 будут очень малыми, амплитуда колебаний и коэффициент нарастания колебаний будут очень большими. В этом случае даже небольшая возмущающая сила может вызвать высокие напряжения (явление резонанса).
будут очень малыми, амплитуда колебаний и коэффициент нарастания колебаний будут очень большими. В этом случае даже небольшая возмущающая сила может вызвать высокие напряжения (явление резонанса).
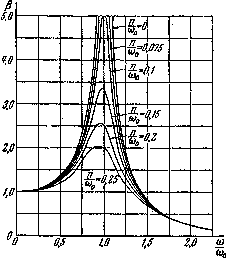
Рис.3. Амплитудно-частотные характеристики системы.
С увеличением сил сопротивления явление резонанса становится все менее заметным. Заметим, однако, что силы сопротивления значительно уменьшают величину амплитуды вынужденных колебаний только вблизи от резонанса 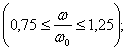 при других величинах отношения — влияние сил сопротивления незначительно.
при других величинах отношения — влияние сил сопротивления незначительно.
Из рис. 3 видно, что если частота 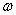 изменения возмущающей силы S очень мала, то амплитуда колебаний приближается к величине
изменения возмущающей силы S очень мала, то амплитуда колебаний приближается к величине 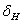 , коэффициент нарастания колебаний стремится к единице и наибольшие напряжения в системе могут быть вычислены как статические напряжения от груза Q и наибольшего значения возмущающей силы S.При очень большой частоте изменения возмущающей силы S амплитуда колебаний и коэффициент нарастания колебаний стремятся к нулю, груз Q можно рассматривать как неподвижный; поэтому наибольшее напряжение в системе равно статическому напряжению от груза Q.
, коэффициент нарастания колебаний стремится к единице и наибольшие напряжения в системе могут быть вычислены как статические напряжения от груза Q и наибольшего значения возмущающей силы S.При очень большой частоте изменения возмущающей силы S амплитуда колебаний и коэффициент нарастания колебаний стремятся к нулю, груз Q можно рассматривать как неподвижный; поэтому наибольшее напряжение в системе равно статическому напряжению от груза Q.
Это обстоятельство имеет очень большое практическое значение; оно используется при конструировании разного рода поглотителей колебаний, сейсмографов, вибрографов и других приборов. В машиностроении амортизаторы, предохраняющие основания машин от усилий, возникающих при колебаниях, подбираются так, чтобы частота собственных колебаний машины на амортизаторах была значительно меньше частоты изменения возмущающей силы.
Дата добавления: 2016-03-05; просмотров: 791;
